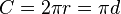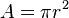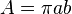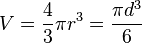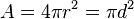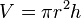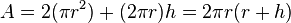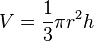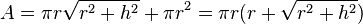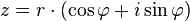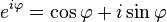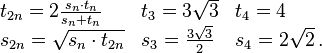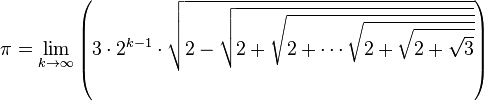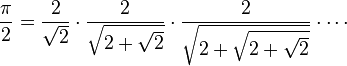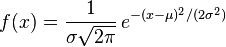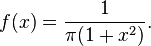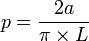Pi - Définition

Utilisation en mathématiques et en sciences

Géométrie

π apparaît dans de nombreuses formules de géométrie impliquant les cercles et les sphères :

Forme géométrique	Formule
Circonférence d’un cercle de rayon r et de diamètre d
Aire d’un disque de rayon r
Aire d’une ellipse de demi-axes a et b
Volume d’une boule de rayon r
Aire surfacique d’une sphère de rayon r
Volume d’un cylindre de hauteur h et de rayon r
Aire surfacique d’un cylindre de hauteur h et de rayon r
Volume d’un cône de hauteur h et de rayon r
Aire surfacique d’un cône de hauteur h et de rayon r

π se retrouve aussi dans le calcul des surfaces et volumes des hypersphères (à plus de 3 dimensions).

Nombres complexes

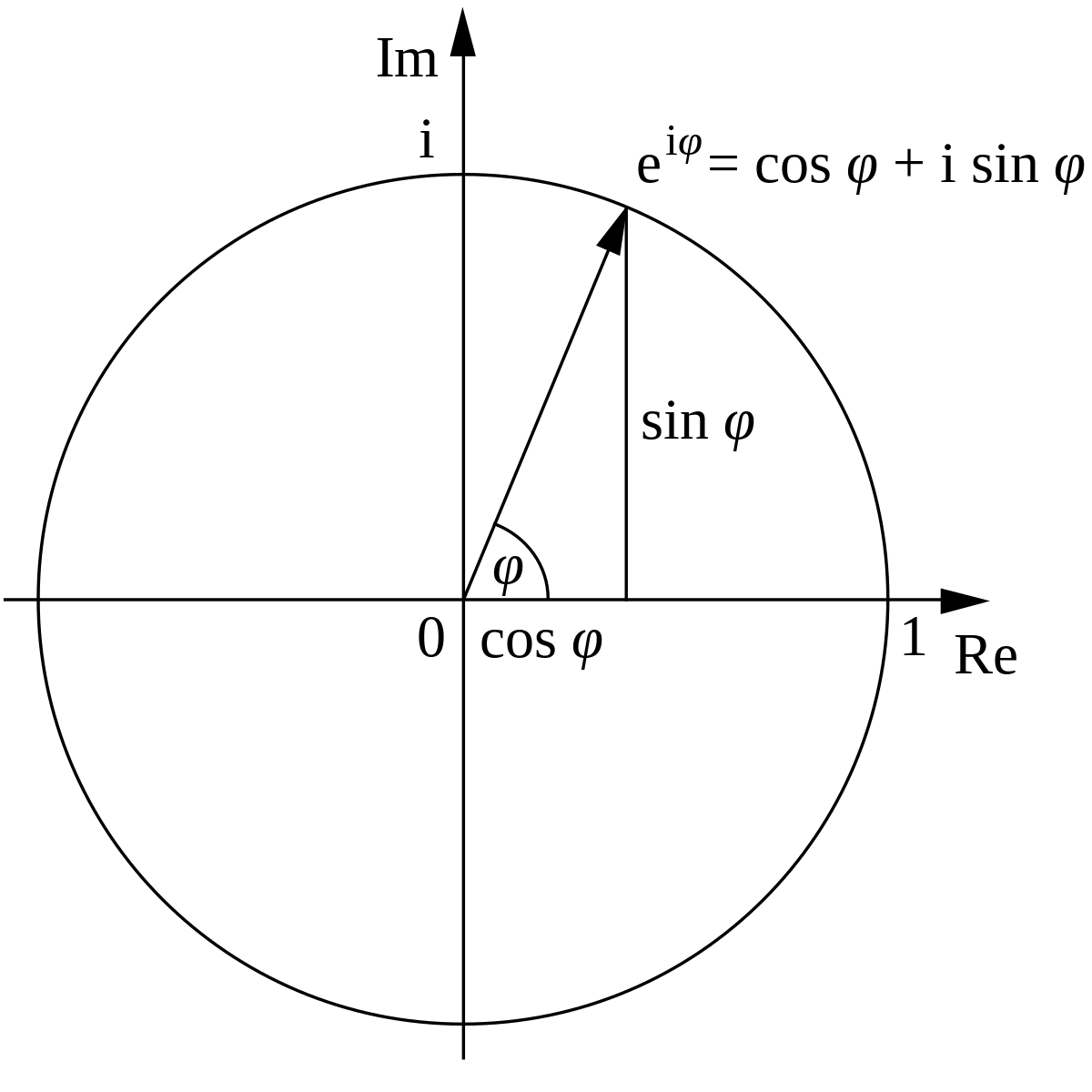
Un nombre complexe z peut s'exprimer en coordonnées polaires de la façon suivante :

L'apparition fréquente de π en analyse complexe a pour origine le comportement de la fonction exponentielle complexe, décrite par la formule d'Euler

où i est l'unité imaginaire satisfaisant la relation i² = −1 et e ≈ 2.71828 est la constante de Néper. Cette formule implique que les puissances imaginaires de e décrivent des rotations sur le cercle unité du plan complexe ; ces rotations ont une période de 360°=2π. En particulier, une rotation de 180°=π donne l'identité d'Euler

et donc

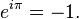
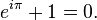
Cette formule a été qualifiée de « formule la plus remarquable des mathématiques » par Richard Feynman, car elle réunit en seulement 7 caractères l'addition, la multiplication, l'exponentiation, l'égalité et les constantes remarquables 0, 1, e, i et π.

Suites et séries

De nombreuses suites ou séries convergent vers π ou un multiple rationnel de π et sont même à l’origine de calculs de valeurs approchées de ce nombre.

Méthode d’Archimède

.

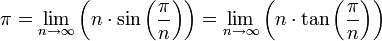
Les deux suites définies par , et , n ≥ 3, représentent les demi-périmètres des polygones réguliers à n côtés, inscrit dans le cercle trigonométrique pour s_n, exinscrit pour t_n. On les exploite par des suites extraites dont l’indice (le nombre de côtés du polygone) double à chaque itération, pour obtenir π par passage à la limite d’expressions utilisant les opérations arithmétiques élémentaires et la racine carrée. Ainsi on peut s’inspirer de la méthode utilisée par Archimède — voir historique du calcul de π — pour donner une définition par récurrence des suites extraites de termes et ou encore et , à l’aide des identités trigonométriques usuelles :

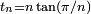
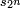
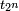
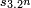
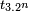
En utilisant les identités trigonométriques, et (x ∈ [0,π]), on peut exprimer s_2^k+1 et s_3.2^k (k≥1) par emboîtements successifs de racines carrées. On obtient les formules qui suivent pour π.

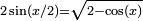
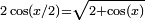
π peut alors s’exprimer sous la forme d’une formule où s'emboîtent des racines carrées :

(k est le nombre de racines carrées emboitées)

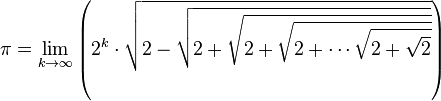
ou encore :

Une autre expression de s_2^k+1, qui peut se déduire simplement de la première de ces deux égalités (multiplier par √(2+√…)), conduit au produit infini suivant (formule de François Viète, 1593).

Sommes et produits infinis

• (formule de Leibniz, James Gregory et Madhava de Sangamagrama)

• (produit de Wallis)

• (formule due à Ramanujan)

• (formule due à David et Gregory Chudnovsky)

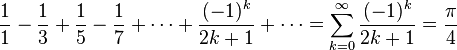
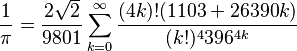
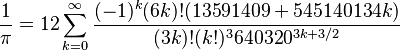
Fonction zêta de Riemann

• (Euler)

• ,

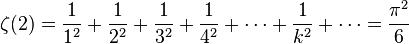
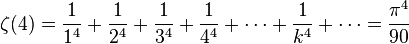
et plus généralement, Euler indiqua que ζ(2n) est un multiple rationnel de π²ⁿ pour un entier positif n.

Suite logistique

Soit (x_n) la suite des itérés de la fonction logistique de paramètre μ = 4 appliquée à un réel x₀ choisi dans l'intervalle [0, 1] (c’est-à-dire qu’on définit, pour tout , ). La suite (x_n) quitte l'intervalle [0;1] et diverge pour quasiment toutes les valeurs initiales.

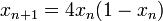
On a pour presque toutes les valeurs initiales x₀.

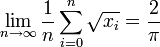
Intégrale

Le nombre π apparait également comme étant le double de la limite du sinus intégral à l'infini :

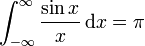
Probabilités et statistiques

En probabilités et en statistiques, il existe de nombreuses lois qui utilisent la constante π, dont :

• la loi normale d'espérance μ et d'écart type σ, dont la densité de probabilité s'écrit :

• la loi normale de Cauchy, dont la densité de probabilité est :

Les deux formules suivantes, tirées de l’analyse, trouvent des applications pratiques en probabilités. L’une permet de montrer la convergence de la loi binomiale vers la loi de Gauss et l’autre permet de calculer la densité d’une loi de Gauss.

• (formule de Stirling)
• 

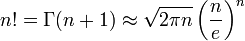
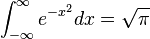
D'autre part, il existe diverses expériences probabilistes où π intervient dans la probabilité théorique. Elles peuvent donc servir, en effectuant un grand nombre d'épreuves, à déterminer une approximation de π.

L’aiguille de Buffon est une expérience de probabilité proposée par Georges-Louis Leclerc, comte de Buffon et consistant à calculer la probabilité qu’une aiguille de longueur a, lancée sur une parquet fait de lattes de largeur L, soit à cheval sur deux lattes, cette probabilité p est :

Cette formule peut être utilisée pour déterminer une valeur approchée de π :

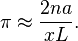
où n est le nombre d'aiguilles lancées, et x celui d'aiguilles qui sont sur deux lattes à la fois.

Cette méthode présente rapidement ses limites ; bien que le résultat soit mathématiquement correct, il ne peut pas être utilisé pour déterminer plus que quelques décimales de π expérimentalement. Pour obtenir seulement une valeur approchée de 3,14, il est nécessaire d'effectuer des millions de lancers, et le nombre de lancers nécessaires croît exponentiellement avec le nombre de décimales voulu. De plus, une très faible erreur dans la mesure des longueurs L et a va se répercuter de façon importante sur la valeur trouvée de π. Par exemple, une différence de mesure d'un seul atome sur une aiguille de longueur de 10 centimètres va se retrouver dès la neuvième décimale de π. En pratique, les cas où l'aiguille semble toucher exactement la limite entre deux lattes va accroître l'imprécision de l'expérience, de sorte que les erreurs apparaîtront bien avant la neuvième décimale.

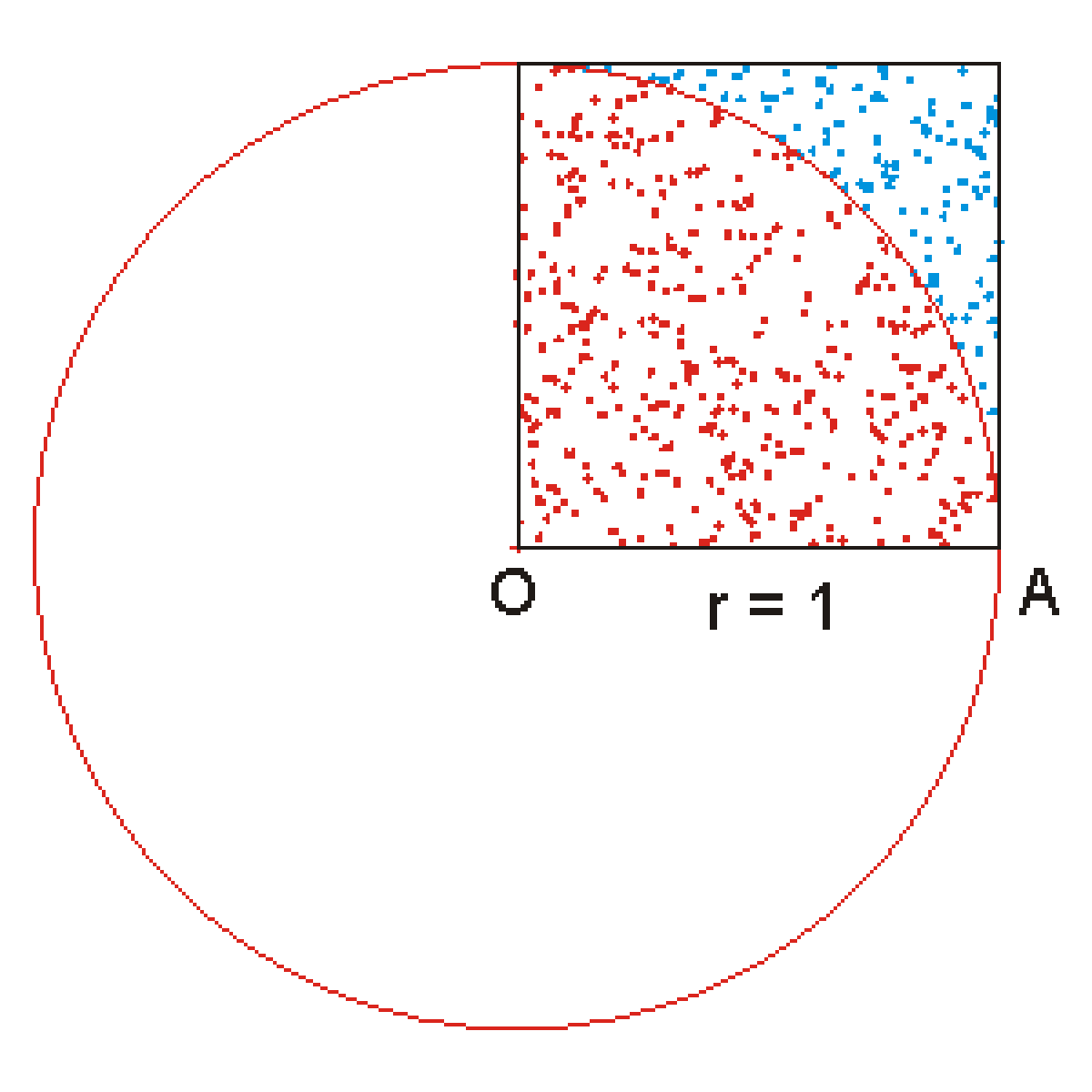
La méthode de Monte Carlo est une autre expérience probabiliste qui consiste à prendre au hasard un point dans un carré de côté 1, la probablité que ce point soit dans le quart de disque de rayon 1 étant de π/4 ; ceci peut facilement se comprendre étant donné que la superficie de ce quart de cercle est π/4 alors que la superficie du carré est 1.