Perspective (perception visuelle) - Définition

Introduction

La perspective visuelle ou oculaire est l’ensemble des transformations par lesquelles une portion du monde spatial tridimensionnel (et euclidien à l’échelle de l’homme) est perçue par la surface bidimensionnelle et courbe (donc non-euclidienne) de l’œil, indépendamment des propriétés stéréoscopiques de la vision binoculaire frontale. Du point de vue mathématique, elle est une projection par laquelle la dimension métrique des objets se trouve convertie en dimension angulaire. La géométrie projective est la branche des mathématiques qui modélise les propriétés de cette projection, indépendamment de la réalité physiologique l'œil.

Notions générales

L’œil considéré individuellement (vision monoculaire) fonctionne comme une lentille stigmatique qui fait correspondre à chaque point de l’espace du cône de vision un point sur la surface rétinienne.

Un même objet apparaît de façon différente à l’œil en fonction de 3 paramètres :

• sa distance à l’œil
• son excentration par rapport à l’axe du regard
• son inclinaison dans les 3 directions

Un segment placé devant soi apparaît d’autant plus grand qu’il est proche, et qu’il se situe dans un plan perpendiculaire à l’axe du regard. Il apparaît d’autant plus courbe qu’il est proche, et qu’il est excentré par rapport à l’axe du regard.

Le processus cognitif par lequel le cerveau reconstruit mentalement dans l’espace les formes des objets perçus sur la surface de la rétine participe si étroitement à l’expérience visuelle qu’il demeure largement pré-conscient. On perçoit comme parallèles deux rails de train, alors qu’on constate bien sur une photographie que leurs lignes se rejoignent à l’horizon, et qu’elles sont toujours incurvées en cloche (vers l’intérieur).

Lois de la perspective

illustration 2 : apparence visuelle d’un segment AB dans l’espace. L’illustration permet de vérifier que la perspective est une application qui fait correspondre à des mesures métriques dans l’espace des mesures angulaires sur une surface. Cette projection est surjective, puisque plusieurs objets distincts de l’espace (ici AiBi, AjBi, AjBj) peuvent avoir la même projection (c’est-à-dire une apparence) en perspective, et inversement, une seule forme apparente correspond à un nombre infini d’objets possibles dans l’espace.

Illustration 3 : apparence courbe des segments de l’espace. C’est en o et seulement en o que le plan est orthogonal à l’axe du regard. Par simple application du théorème de Pythagore, OA= (oO2+oA2)1/2 et Oi = (oO2+oi2)1/2 Donc oO < (iO = jO) < (AO = BO =CO = DO) Un segment apparaissant d’autant plus petit qu’il est éloigné, on en déduit que AD apparaît plus petite que ij, et que, de façon générale, pour tout couplet (x, y ; x є AB ; y є CD ; xy ║AD), xy décroît tandis que xi croît. On en déduit que les côtés du carré, et de façon générale toute droite du plan ne passant pas par o, apparaissent en perspective sous forme de courbes en cloche placées entre leur « original réel» et O et qui tendent en leur 2 extrémités vers la droite parallèle à leur « original » passant par o.

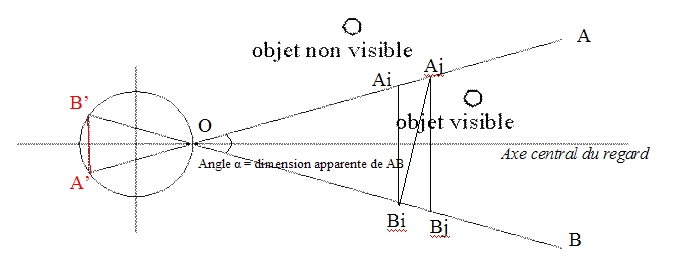
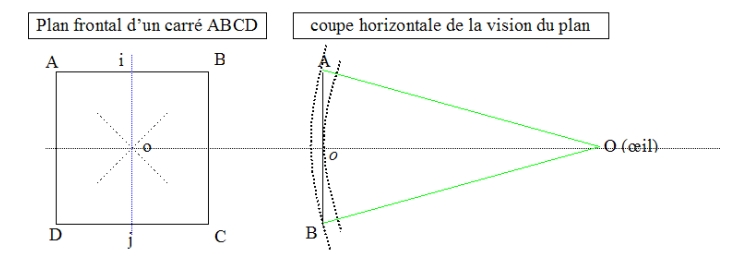
Les illustrations 2 et 3 permettent de se convaincre des principes suivants :

• A inclinaison constante, la dimension apparente d’un segment est fonction inverse de sa distance à l’œil

• A distance constante, la dimension apparente d’un segment décroît tandis qu’augmente l’angle d’inclinaison du segment par rapport au plan perpendiculaire au regard

• Tout segment de l’espace qui ne passe pas par le centre du regard apparaît courbé en perspective ; l’intensité de la courbure croît avec l’excentration.

De ces principes fondamentaux se déduisent des principes plus complexes pour les solides visibles. Par exemple :

• Deux droites parallèles dans l’espace réel apparaissent en perspective comme des courbes en cloche convergeant vers le même point (qui peut être à l’intérieur comme à l’extérieur de l’ellipse visuelle).

• Une surface carrée perpendiculaire à l’axe du regard dans le monde réel apparaît en perspective comme un quasi-trapèze dont aucun des angles n’est droit, et dont les côtés sont incurvés en cloche vers l’extérieur du regard.

• Plus une surface carrée est proche (i.e. envahit le champ visuel), plus son apparence est déformée en termes d’angles et de courbures. Plus elle s’éloigne (i.e. rétrécit), plus elle prend l’apparence simple d’une projection euclidienne d’une espace sur un plan.

• un cube dont aucune des faces n’est parallèle à l’axe du regard présente forcément 3 faces, dont aucun angle n’est droit, et dont les 9 arêtes visibles sont des courbes qui convergent 3 par 3 vers 3 points.