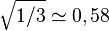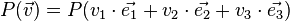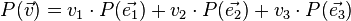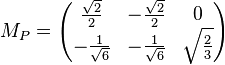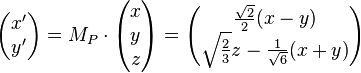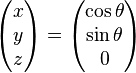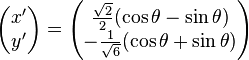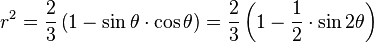Perspective isométrique - Définition

Approche mathématique

La perspective isométrique est en fait une projection sur un plan selon un axe orthogonal à ce plan : une projection orthogonale. C'est une application linéaire. une perspective est une mise en plan dans différentes vues dans l'espace. Une isométrie se perçoit 120°.

Facteur de report sur les axes

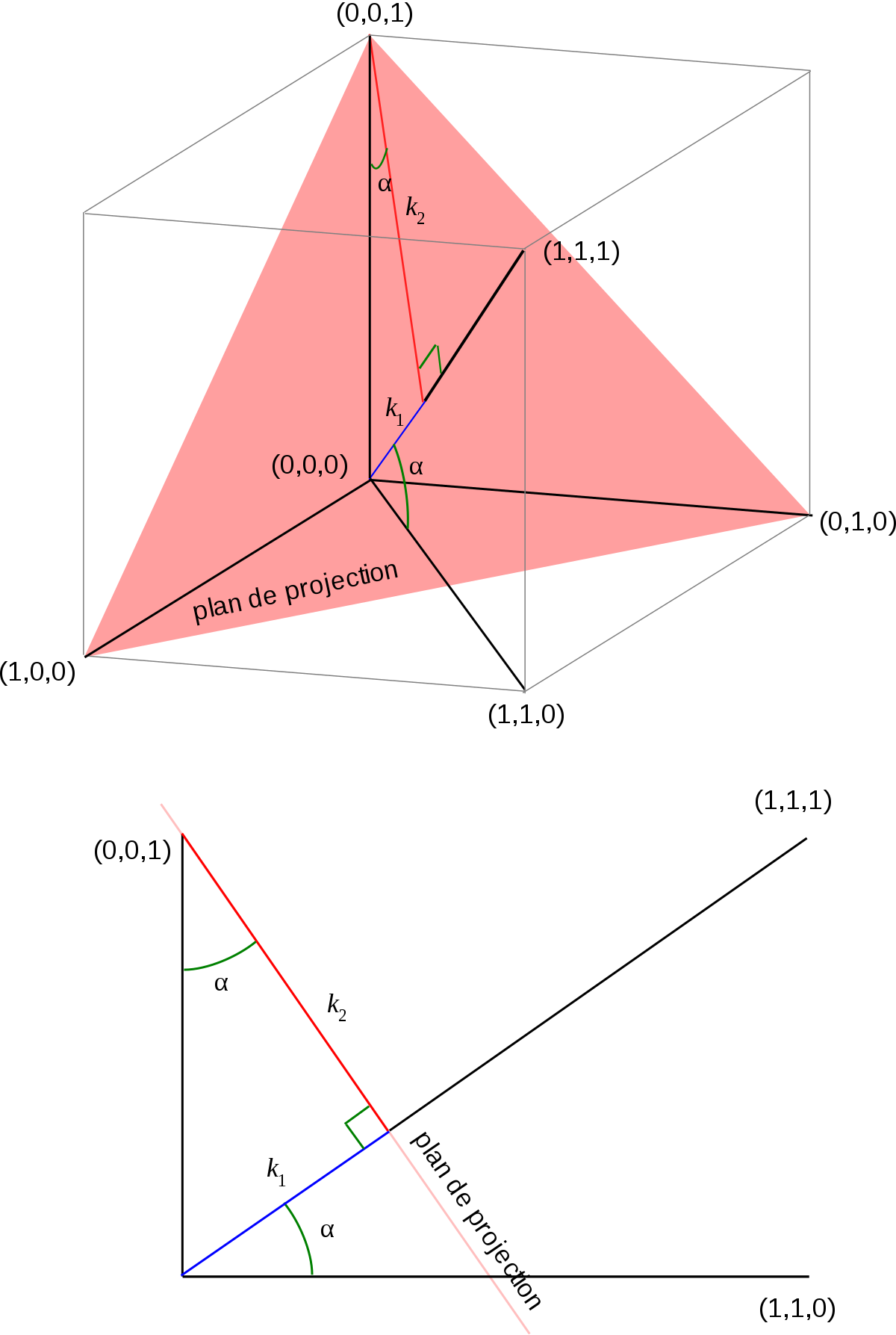
On peut calculer le facteur de proportionnalité sur les axes simplement grâce à la trigonométrie :

• considérons l'arête du cube qui va de l'origine au point (0,0,1) ; elle fait un angle α avec le plan de projection, le projeté a donc une longueur de cos α ;
• α est aussi l'angle entre la normale au plan de projection passant par l'origine et par le point (1,1,1), et la bissectrice des axes x et y qui passe par (1,1,0) ;
• dans le triangle formé par les points (0,0,0), (1,1,0) et (1,1,1) est un triangle rectangle ; le segment [(0,0,0), (1,1,0)] a pour longueur √2 (diagonale du carré), le segment [(1,1,0), (1,1,1)] a pour longueur 1, et l'hypoténuse [(0,0,0), (1,1,1)] a pour longueur √3

On a donc

.

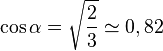
On en déduit que α ≈ 35,26 °.

On peut aussi utiliser le produit scalaire :

• le vecteur unitaire porté par la grande diagonale est (1/√3, 1/√3, 1/√3) ;
• l'arête [(0,0,0), (0,0,1)] se projette sur la grande diagonale en un segment de longueur k₁, et sur le plan normal à cette grande diagonale en un segment de longueur k₂
• k₁ est le produit scalaire de et de , et peut se calculer avec les coordonnées :
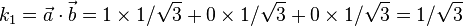
• le théorème de Pythagore nous indique que k₁² + k₂² = 1 (longueur de l'arête du cube).

On a donc :

.

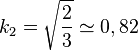
Les longueurs des segments sur les axes du repère se projettent donc avec un facteur de 0,82.

On arrive également à cette conclusion en utilisant la formule générale des projections orthogonales, voir Perspective axonométrique > Perspective isométrique.

Par ailleurs, si l'on considère le cercle unité du plan (x, y), le rayon se projetant selon la ligne de plus grande pente est la première bissectrice du plan, avec un facteur de projection valant sin α = k₁ = 1/√3 ≈ 0,58, ce qui correspond au petit axe de l'ellipse.

Transformation des coordonnées

La transformation des coordonnées cartésienne est utilisée pour calculer les vues à partir des coordonnées des points, par exemple dans le cas de jeux vidéo ou de logiciels de représentation graphique 3D.

Supposons l'espace muni d'une base orthonormée directe . La projection P se fait selon le vecteur de composantes (1,1,1), c'est-à-dire le vecteur , selon le plan représenté par ce même vecteur.

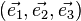
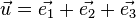
Comme toute application linéaire, elle peut être représentée par la transformation des vecteurs de la base, puisqu'un vecteur quelconque se transforme selon

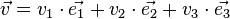
Soit . Appelons la base orthonormée directe dans le plan de projection. On choisit arbitrairement que fait un angle de -π/6 avec .

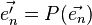
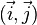
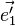
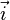
L'application des calculs pour les projections orthogonales au cas particulier de la perspective isométrique nous donne (voir Perspective axonométrique > Perspective isométrique) :

•  ;
•  ; k₂ = k₁
•  ; k₃ = k₁

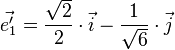
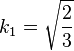
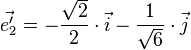
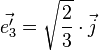
La matrice de la projection M_P est donc

Considérons un point (x, y, z) de l'espace qui se projette en (x', y'). Sa projection sera donc :

Voir aussi Projection (géométrie) > Projection sur un plan parallèlement à une droite en géométrie analytique.

Transformation d'un cercle d'un plan contenant deux axes

Considérons le cercle trigonométrique du plan . Les coordonnées paramétriques de ses points sont :

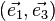
Les coordonnées des points projetés dans la base sont donc

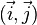
La distance à l'origine est , soit

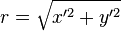
(formule de De Moivre) ; ceci fournit au passage une équation paramétrique de l'ellipse. Cette distance varie donc entre 1 et . On retrouve les rapports du grand axe et du petit axe de l'ellipse.