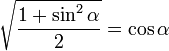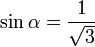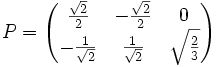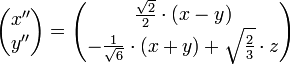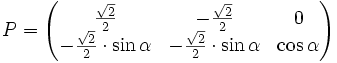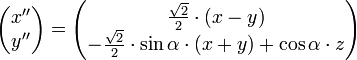Perspective axonométrique - Définition
La liste des auteurs de cet article est disponible ici.
Formalisme
Considérons un repère orthonormé direct
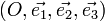
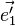
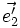
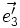
- la représentation de
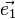
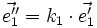
- la représentation de
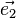
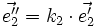
- la représentation de
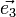
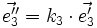
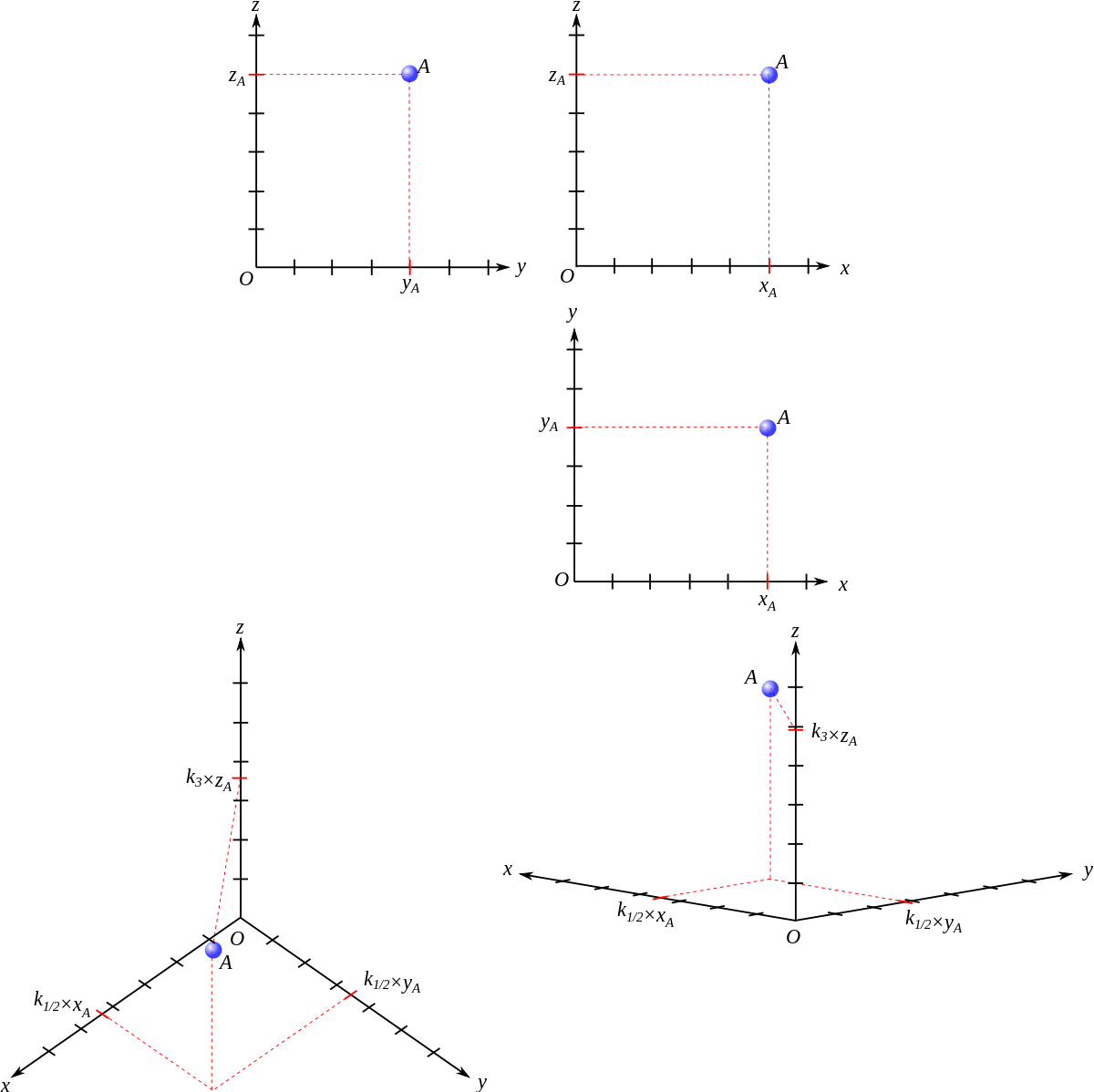
Si l'on connaît les coordonnées (x, y, z) d'un point dans l'espace, alors le placement de ce point sur le plan de projection est particulièrement simple : il suffit de reporter ces coordonnées sur les axes projetés en appliquant les coefficients k1, k2 et k3.
Perspective isométrique
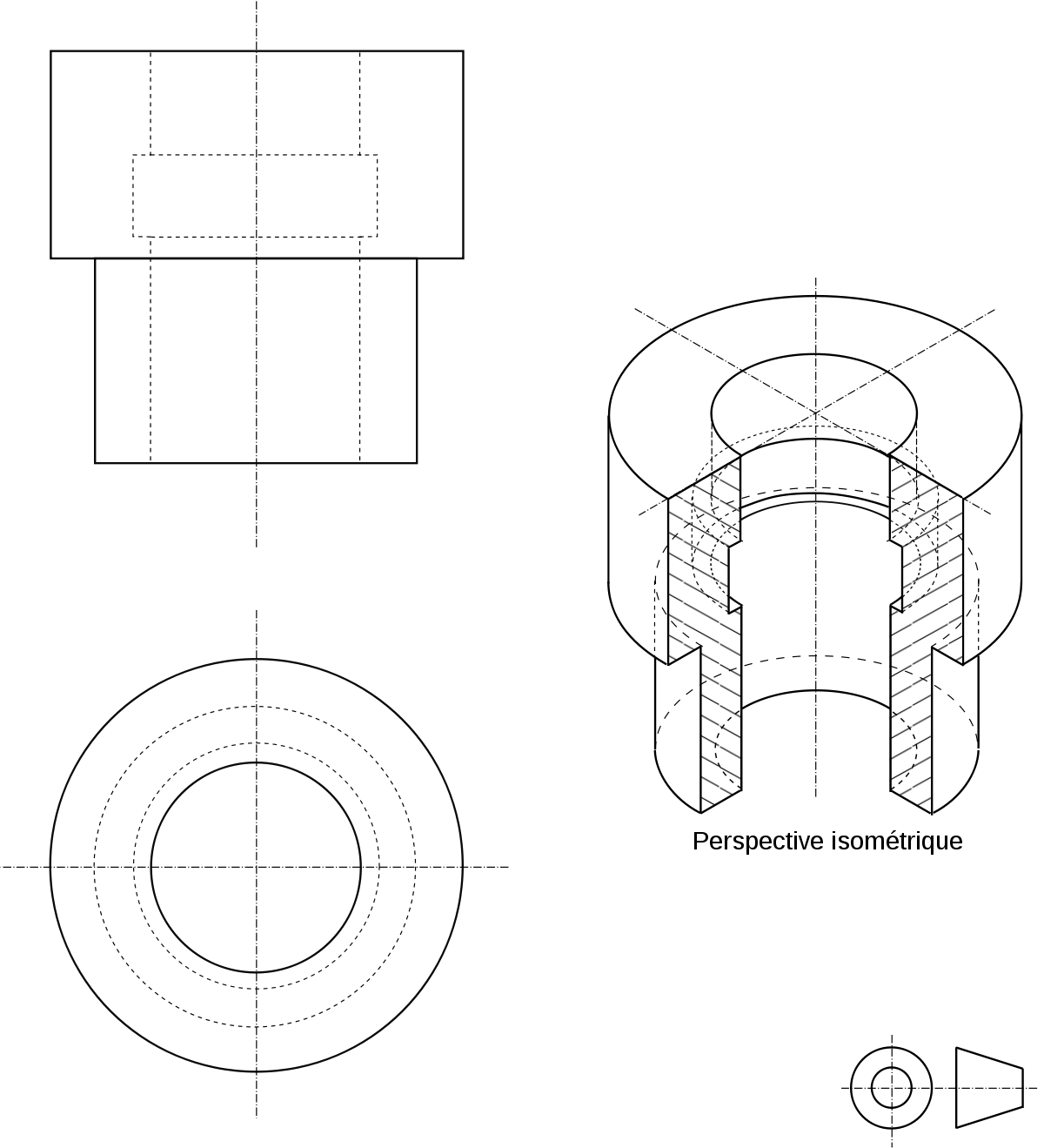
La perspective isométrique est le cas particulier où les trois rapports sont égaux. Il s'agit d'une projection orthogonale.
On a :
- k1 = k3
soit
en utilisant le fait que cos²α + sin²α = 1, on obtient
et donc également
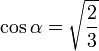
- Ox :
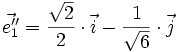
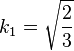
- Oy :
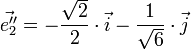
- Oz :
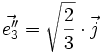
Il s'agit donc d'un projection orthogonale dimétrique (ω = 45 °), pour laquelle on a α ≈ 35,26 ° et k1 = k2 = k3 ≈ 0,82.
et
soit
- x" ≈ 0,71·(x - y )
- y" ≈ -0,41·(x + y ) + 0,82·z
Voir l'article détaillé Perspective isométrique.
Perspectives dimétriques
Une perspective dimétrique est une perspective pour laquelle deux des rapports sont égaux.
Géométrie descriptive
Les vues en géométrie descriptive sont un cas particulier dans lequel deux des coefficients sont égaux à 1, et le troisième coefficient est égal à 0.
Ce sont également des projections orthogonales.
Perspective cavalière
Il s'agit d'une projection oblique et non d'une véritable axonométrie.
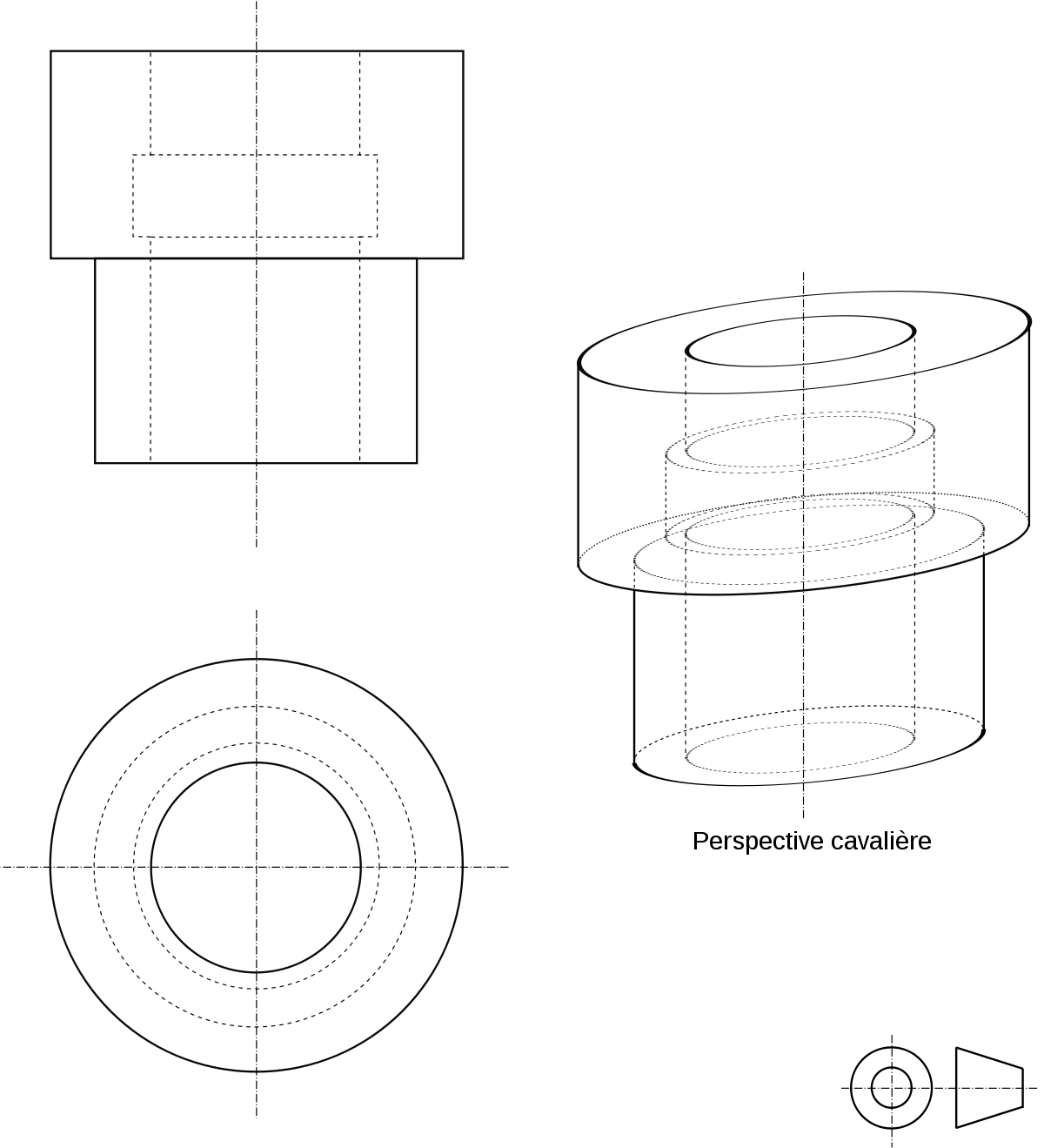
Dans la perspective cavalière, deux des axes sont orthogonaux et ont un facteur de report de 1. Le troisième axe est incliné, en général de 30 ou 45° par rapport à l'horizontale, appelé « angle de fuite », et a un facteur de report inférieur à 1, en général 0,7 ou 0,5.
Voir l'article détaillé Perspective cavalière.
Projections orthogonales dimétriques
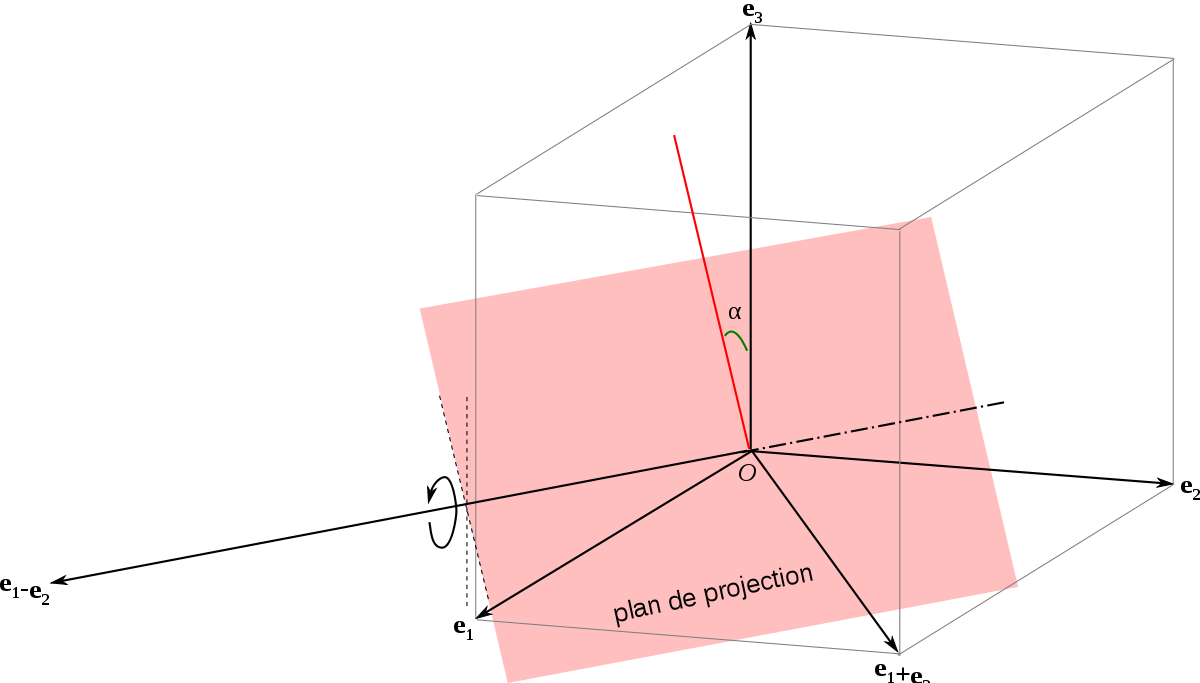
Choisissons k1 = k2 ; les projections des axes x et y sont symétriques par rapport à la verticale. Cette situation est un cas particulier de la projection orthogonale avec ω = 45 ° ; on a cos ω = sin ω = √2/2, soit
- Ox : ;
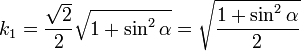
- Oy :
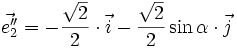
- Oz : ; k3 = | cosα | .
Le plan de projection tourne autour de la deuxième bissectrice du plan (Oxy), c'est-à-dire autour du vecteur
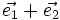
On a
et
Par exemple, pour α = 45 °, on a
- k3 ≈ 0,71 ;
- k1 = k2 ≈ 0,87 ;
- (i, e"1 ) ≈ 35,26 ° (vecteur e"1 dirigé vers le bas) ;
et pour α = -10 °, on a
- k3 ≈ 0,98 ;
- k1 = k2 ≈ 0,72 ;
- (i, e"1 ) ≈ 9,85 (vecteur e"1 dirigé vers le haut).