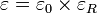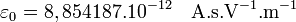Permittivité - Définition
La liste des auteurs de cet article est disponible ici.
Permittivité du vide et permittivité relative
La permittivité d’un milieu peut aussi être exprimée par une quantité adimensionnelle : la permittivité relative ou « constante diélectrique », normalisée par rapport à un milieu de référence :
avec
-

-
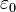
-
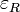
Le vide est choisi comme milieu de référence, car il est linéaire, homogène, isotropique, et avec réponse instantanée, et car avec ces propriétés, la permittivité du vide devient une constante :
Ce vide de référence est un vide absolu et théorique, qui ne peut être obtenu en pratique de façon expérimentale. Dans nombre d’expériences, on admet cependant un gaz neutre à faible pression (comme l’air, ou mieux un halogène) comme suffisant pour approcher le vide. Dans d’autres cas (notamment si le gaz peut être ionisé ou si la faible pression du vide approché expérimentalement est suffisante pour fausser les résultats), on tiendra compte de la permittivité relative de ce gaz.
Relations avec d'autres propriétés physiques
Permittivité et susceptibilité
La susceptibilité électrique χ est un nombre sans dimension tel que
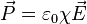
Permittivité et polarisabilité
La permittivité est une grandeur macroscopique ; la polarisabilité est définie pour un atome ou une molécule. Sous certaines hypothèses, il est possible de relier les deux : c'est la formule de Clausius-Mossotti.
Célérité de la lumière dans le vide
Constante de structure fine
Permittivité complexe
Dans un milieu diélectrique réel, il existe toujours à basses fréquences une faible conductivité liée à différents mécanismes microscopiques (défauts notamment). On parle alors de pertes diélectriques. On peut tenir compte de ces pertes en définissant une permittivité complexe :
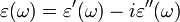
Ces pertes sont souvent très faibles. La partie imaginaire est donc très petite devant la partie réelle. On parle alors parfois d'angle de perte, exprimé en pour cents et défini par :
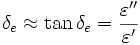
Cette appellation s'explique par le fait que cet angle δe est l'angle formé par les vecteurs champ électrique et déplacement électrique dans le plan complexe.
Les parties réelles et imaginaires de la permittivité ne sont pas complètement indépendantes. Elles sont reliées par les relations de Kramers-Kronig.