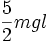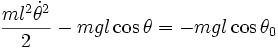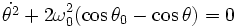Pendule simple - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
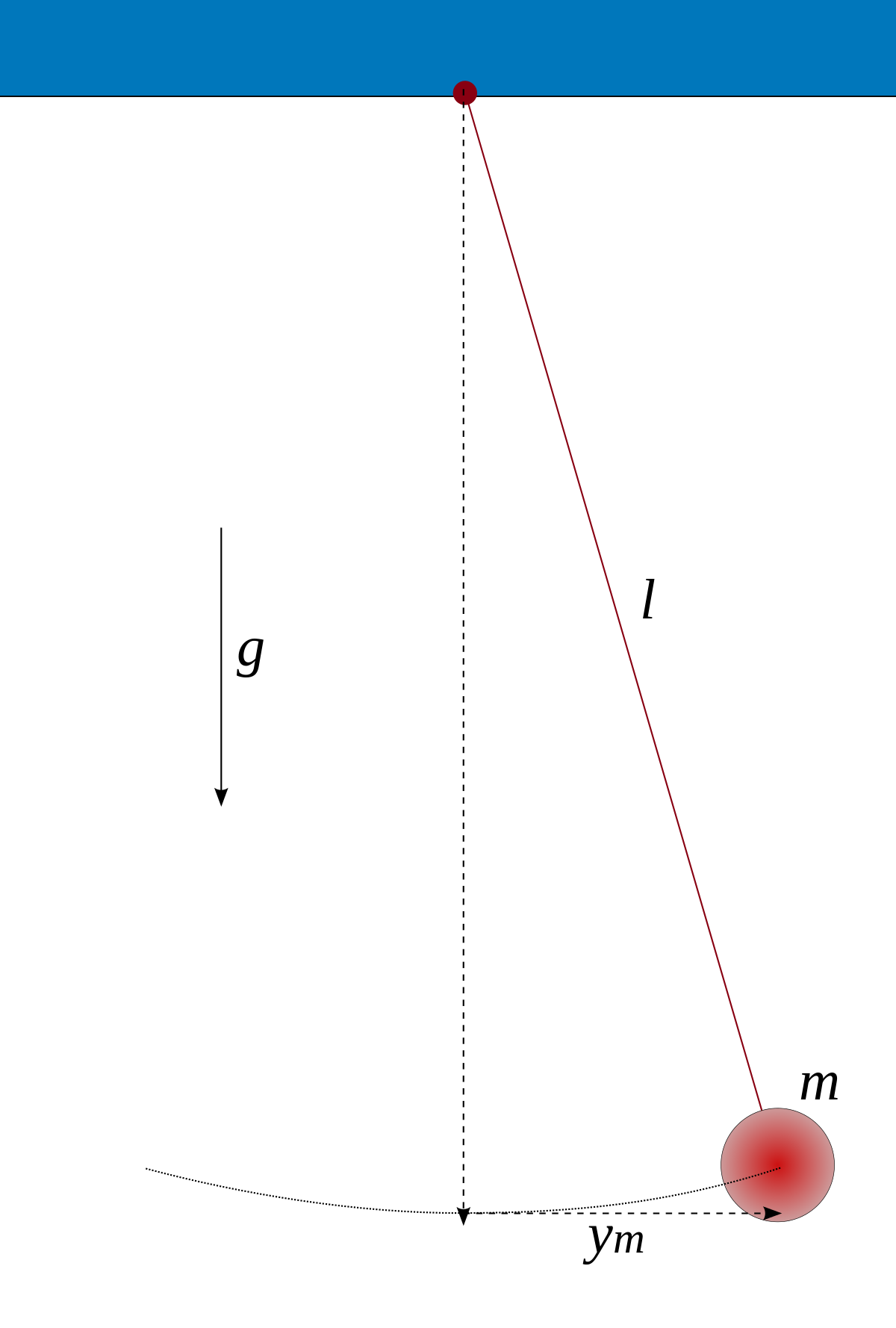
En physique, le pendule simple est une masse ponctuelle fixée à l'extrémité d'un fil sans masse, inextensible et sans raideur et oscillant sous l'effet de la pesanteur. Il s'agit du modèle de pendule pesant le plus simple. Il est parfois appelé pendule de gravité idéal et, par opposition, tout pendule de gravité réel est appelé pendule pesant composé. Par extension on appelle aussi parfois pendule simple un dispositif dans lequel le fil inextensible et remplacé par une tige rigide de masse nulle pouvant tourner sans frottement dans un plan vertical autour de son extrémité fixe (liaison parfaite).
Il est possible d'approcher expérimentalement cet objet théorique en suspendant une masse de faible dimension au bout d'un fil (voir illustration). À cause de sa nature relativement simple, il se prête à des études théoriques poussées sur le plan mathématique. Ces études ont trouvé plusieurs applications en physique théorique, notamment dans les systèmes harmoniques simples.
Sous l'effet de son poids, lorsque le pendule est écarté de sa position d'équilibre (la verticale), le point matériel de masse m se déplace sur un arc de cercle : l'effet du poids tendant constamment à ramener le pendule vers sa position d'équilibre stable, celui-ci se met à osciller.
Les équations du mouvement
Mise en équation
On repère la position du pendule simple par l'angle qu'il fait avec la verticale descendante. On choisit une orientation positive : la position de la masse est donc repérée par l'élongation angulaire algébrique
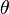
On note
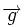
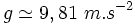
Bilan des forces :
- Le poids
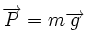
- La tension
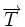
Dans ce modèle les autres forces sont oubliées, notamment les forces de frottement ; or un pendule s'arrête d'osciller sous l'action des frottements : le mouvement perpétuel n'existe pas à cette échelle d'énergie.
Énergie mécanique du pendule :
- La somme de l'énergie cinétique du pendule et de son énergie potentielle de pesanteur, mesurée à partir du point le plus bas vaut (la vitesse de la masse valant
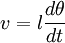
-
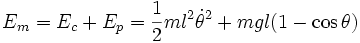
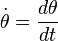
- Puisque la tension de la tige est à tout instant perpendiculaire au mouvement circulaire de G, cette force exerce un travail nul. De plus comme le poids est une force conservative et que toute autre force est négligée, l’énergie mécanique du système est conservée. Dire que cette quantité est conservée au cours du mouvement, c'est dire que sa valeur est constante au cours du temps, ou encore que sa variation est nulle à tout instant. Ceci peut se traduire mathématiquement en écrivant que la dérivée par rapport au temps est nulle. On obtient alors :
-
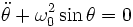
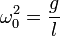
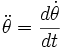
- Cette équation peut également être déduite du Principe Fondamental de la Dynamique, en projetant les deux forces
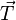
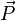
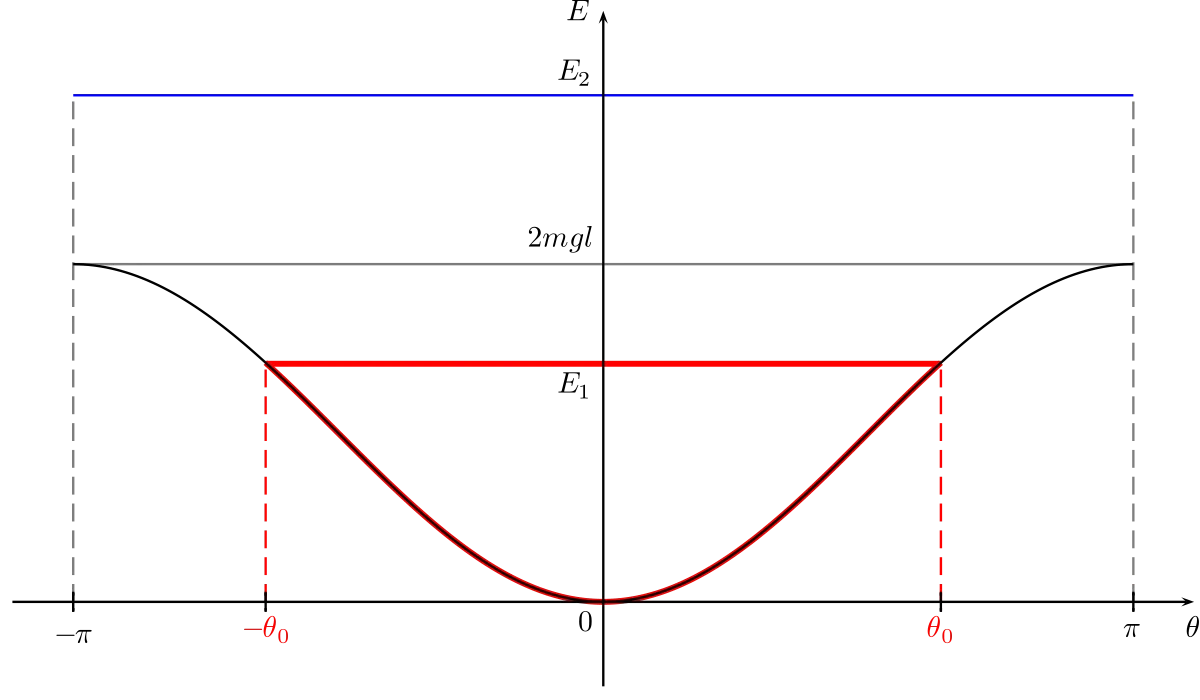
Puits de potentiel :
Si on trace en fonction de θ le graphe de l'énergie potentielle
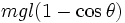
- Si l'énergie mécanique E du pendule se situe à un niveau E1 inférieur à 2mgl, le pendule est confiné dans un puits de potentiel. Il existe une élongation maximale θ0 du pendule pour laquelle la vitesse s'annule, et le pendule oscille périodiquement. On a alors :
qui se simplifie en :
- Si l'énergie E du pendule se situe à un niveau E2 supérieur à 2mgl, alors le pendule franchit les barrières de potentiel, sa vitesse angulaire ne peut s'annuler et le pendule tourne autour du point O.
Résolution
La résolution des équations du mouvement du pendule simple n'est pas aisé. Le pendule cycloïdal de Huygens représente un mouvement dans un puits de potentiel plus facile à résoudre. Le pendule simple discret propose une approche pas à pas de la résolution.
1/ pour de petites oscillations, on peut confondre sin(θ) avec θ. On obtient alors l'équation :
-
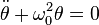
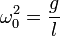
dont une solution est :
-
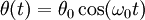
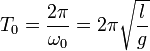
2/ pour de plus grandes amplitudes, on peut utiliser pour la période :
- La :
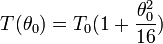
- La formule exacte :
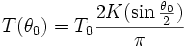
D'autre part, l'oscillation périodique devient nettement anharmonique, comme le montre le taux d'harmoniques.
3/ pour une énergie mécanique supérieure à 2mgl, le pendule tournoie de façon périodique. À grande vitesse V, cette période T tend vers
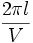
Tension de la tige
Une quantité physique dépend de la masse du pendule : la tension de la tige (pour sa mesure, on peut coller sur la barre une jauge de contrainte étalonnée).
La projection sur la normale (
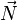
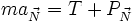
Or l'expression de l'accélération radiale en coordonnées polaires avec une distance à l'origine constante (rayon constant) est
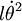
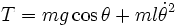
et nous avons vu que
-
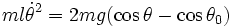
T varie entre
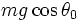
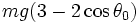
Boucler la boucle
T s'annule pour certaines conditions initiales de lancement différentes de celle proposée ci-dessus, voire devient négative, la tige supportant alors la masse. Il est classique de montrer que, lancée du point le plus bas avec une énergie 2mgl, la masse arrivera au bout d'un temps infini au sommet du cercle (et le cas est intégrable aisément). On se doute que si la tige est remplacée par un fil (liaison unilatérale), la trajectoire ne sera pas : montée au sommet, puis chute à la verticale ; il y aura décrochage quand T sera nulle, c’est-à-dire pour θ tel que
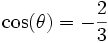
Alors que pour une tige, il suffit que l'énergie E dépasse 2mgl pour que le pendule se mette à tourner (looping the loop), dans le cas d'un fil il faut une énergie cinétique initiale supérieure à