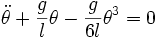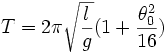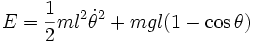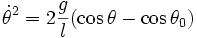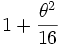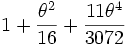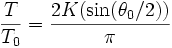Pendule simple - Définition
La liste des auteurs de cet article est disponible ici.
Grandes amplitudes et non linéarité
On introduit progressivement la non-linéarité:
- d'abord en considérant le deuxième terme du développement du sinus.
- puis en traitant le cas général, qui nécessite l'utilisation des fonctions elliptiques de Jacobi K, sn, cn, dn.
Formule de Borda
On considère donc l'équation différentielle approchée, dite de Duffing, obtenue en remplaçant sinθ par
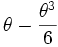
On montre alors que la période dépend de l'amplitude. La formule de Borda donne :
Le terme négligé qui suit est
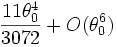
- La méthode des perturbations de Lindstedt-Poincaré consiste à modifier la solution
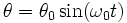
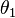
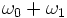
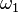
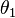
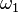
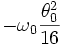
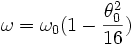
- Si on suppose l'oscillation quasi-sinusoïdale, la raideur moyenne étant plus faible, on s'attend physiquement à une diminution de la pulsation. En utilisant la formule d'Euler
![\sin^3x = {3\over 4} \sin x -[{1 \over 4} \sin(3x)]_\mathrm{omis}](https://static.techno-science.net/illustration/Definitions/autres/8/874e1f66a81d8ce8523e0c990846836d_ebf2474f824666819a2ff276044cd29a.png)
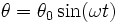
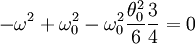
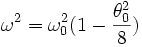
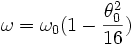
- On peut préférer la démonstration suivante dite du viriel :
 ~
~ 
d'où par la formule de Wallis :
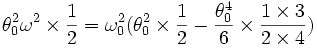
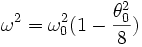
- L'équation du mouvement du pendule est complètement intégrable grâce aux fonctions elliptiques, ce qui fait l'objet du paragraphe qui suit. Il suffit alors d'effectuer un développement à l'ordre souhaité de la solution exacte.
Cas pleinement non-linéaire
On considère le cas pleinement non-linéaire. Ecrivons la conservation de l'énergie mécanique
sous la forme : , avec
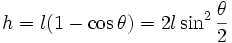
Posons H = 2lk2. Il existe trois cas :
- k < 1 , le pendule oscille : h varie entre 0 et H = l(1 − cosθ0). On a :
Entre 0 et θ0, on a
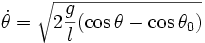
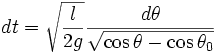
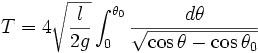
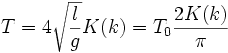
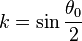
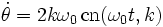
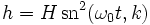
| θ en degré | θ en radian |
|
|
|
|---|---|---|---|---|
| 10 | 0,175 | 1,00 | 1,00 | 1,00 |
| 20 | 0,349 | 1,01 | 1,01 | 1,01 |
| 30 | 0,524 | 1,02 | 1,02 | 1,02 |
| 40 | 0,698 | 1,03 | 1,03 | 1,03 |
| 50 | 0,873 | 1,05 | 1,05 | 1,05 |
| 60 | 1,047 | 1,07 | 1,07 | 1,07 |
| 70 | 1,222 | 1,09 | 1,10 | 1,10 |
| 80 | 1,396 | 1,12 | 1,14 | 1,14 |
| 90 | 1,571 | 1,15 | 1,18 | 1,18 |
| 100 | 1,745 | 1,19 | 1,22 | 1,23 |
| 110 | 1,920 | 1,23 | 1,28 | 1,30 |
| 120 | 2,094 | 1,27 | 1,34 | 1,37 |
| 130 | 2,269 | 1,32 | 1,42 | 1,47 |
| 140 | 2,443 | 1,37 | 1,50 | 1,60 |
| 150 | 2,618 | 1,43 | 1,60 | 1,76 |
| 160 | 2,793 | 1,49 | 1,71 | 2.01 |
| 170 | 2,967 | 1,55 | 1,83 | 2,44 |
| 180 | 3,142 | 1,62 | 1,96 |
|
La fonction K admet également le développement suivant :
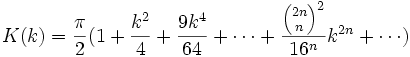
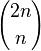
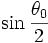
- k = 1 , cas limite correspondant à θ0 = π. On a :
Temps infini pour monter à la verticale
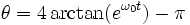
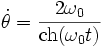
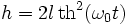
- k > 1 , le pendule tournoie : v2 varie entre 2g(H − 2l) et 2gH. La période pour effectuer un tour est
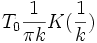
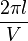
Il est parfois judicieux de prendre pour période le temps mis pour faire deux tours. En effet, pour k légèrement inférieur à 1, le pendule effectue une trajectoire de longueur voisine de 4π. Avec cette convention, on a alors
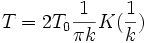
On a également :
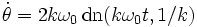
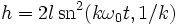
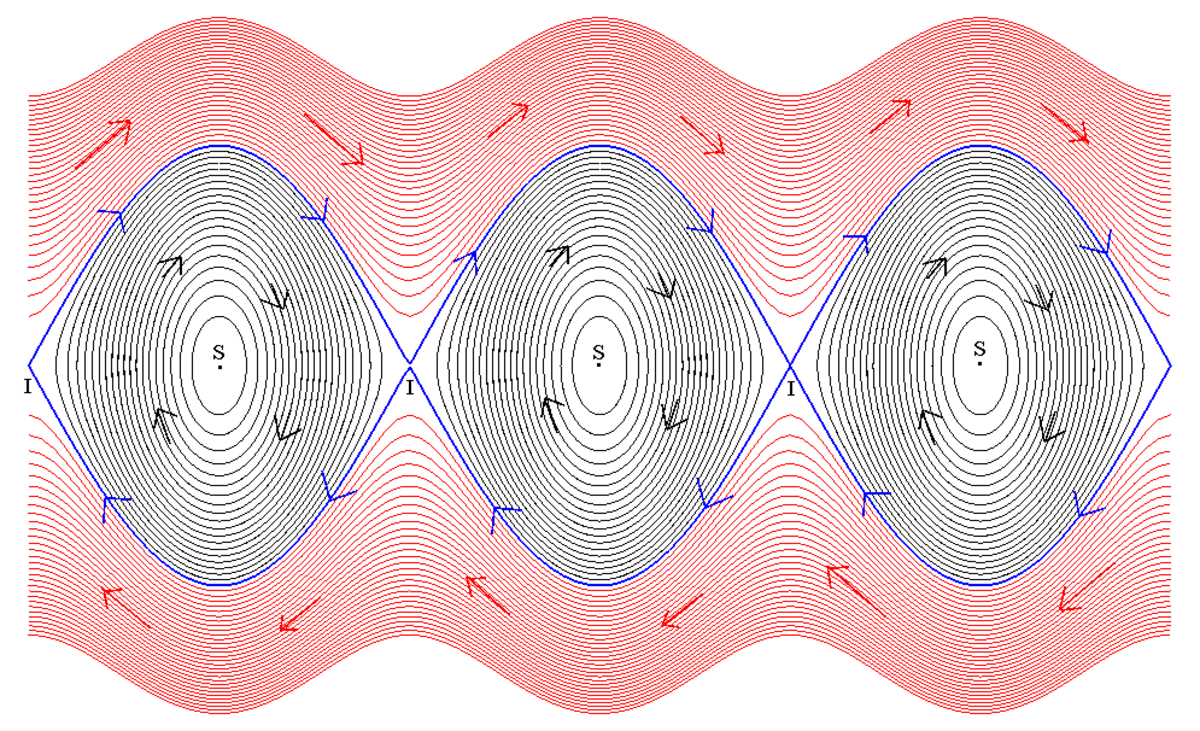
Plan de phase
On appelle orbite de phase la représentation paramétrée en temps du couple (θ(t),
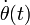
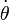
- la région dite d'oscillation (en noir), dite en œil d'Horus ou en œil en amande. Chaque orbite est parcourue dans le sens inverse au sens trigonométrique et tourne autour des points d'équilibre stables S, correspond aux valeurs 0, 2π, 4π, etc de θ0.
- les deux régions de révolution (en rouge) , soit positive (en haut), soit négative (en bas), correspondant au cas où le pendule tourne autour du point O.
- la séparatrice, en bleu, correspondant au cas limite où θ0 vaut π.
- les points d'équilibre stable S déjà évoqués.
- Les points d'équilibre instable I correspondant aux valeurs π, 3π, etc de θ0. Il faut un temps infini pour parcourir une orbite qui va d'un point I à un autre.
Il paraît clair dorénavant que si l'on établit un mécanisme quelconque qui peut soustraire ou ajouter une petite énergie au pendule au voisinage de l'élongation π, on aura un phénomène difficile à prévoir même s'il est déterministe: exemple , placer un tout petit pendule accroché à la masse m: on a ainsi un pendule double ; les oscillations non-linéaires de ce pendule, lesté d'un tel minuscule pendule, laissent pantois quand on les enregistre: Poincaré fut , avec Liapunov , un des premiers à considérer ce genre de problème; puis Birkhoff; puis l'école russe entraînée par la haute figure de Kolmogorov, et puis celle de Bogoliubov et de Krylov, puis Arnold,... jusqu'au moment où un article de 1971 de Ruelle et Takens vînt suggérer que la situation était normale dès que l'espace des phases était à trois dimensions ou plus [on utilise parfois l'expression 1.5 degré de liberté].