Pendule simple - Définition

Étude fine au voisinage de la séparatrice

On s'intéresse au spectre de la vitesse juste au-dessus et au-dessous du niveau énergétique de la séparatrice. Sur cette séparatrice, le spectre est qualifié de mode soliton.

Rappel : la séparatrice et le mode soliton

Dans le cas de la séparatrice , l'équation du premier ordre s'écrit :

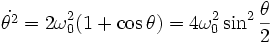avec θ(0) = 0 et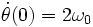

La solution "soliton" est caractérisée par les équations suivantes :

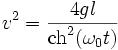
Oscillations longues : 1 - k² << 1

Si l'énergie du pendule est très légèrement inférieure à 2gH, la différence avec le mode soliton est infime. La valeur de la vitesse est imperceptiblement la même et le mouvement est donc quasi-identique, SAUF pour les moments où elle va s'annuler. La période est finie est vaut : , valeur obtenue en utilisant la valeur approchée au voisinage de k = 1.

Tournoiements longs : k² - 1 << 1

De même, si l'énergie est très légèrement supérieure à 2gH, le mouvement est quasi-identique (mode soliton), SAUF que la vitesse ne s'annule jamais et que l'élongation devient fonction monotone en quasi-escalier de marches de hauteur 2π en forme de sigmoïdes (des "kinks" en anglais), longues d'une période très grande mais finie : . Remarquer l'apparition d'un 2 au dénominateur, qui est un artefact dû au fait que dans un cas, on calcule la période sur un aller et retour (soit 4π environ), alors qu'un tournoiement s'effectue sur 2π. C'est une des raisons d'examiner le "pendule à gazette" soigneusement.

Anharmonicité

Vitesse du pendule simple au voisinage de la séparatrice.

On trouve donc que ou sont donc bien les mêmes fonctions de période . Ci-dessous, l'allure de au voisinage de . L'allure du graphe est la même, que soit légèrement supérieur à 1 ou légèrement inférieur.

On caractérise le taux d'anharmonicité par l'étendue du spectre (discret puisque la fonction est périodique). A la limite :

• H = 2l + rien , |v| est

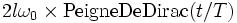
Or, le spectre d'un peigne de Dirac est un peigne de Dirac (théorème de Poisson)

Le pendule simple est l'exemple le plus élémentaire qui montre :

• à faible amplitude: la linéarisation et donc le monochromatisme
• à amplitude critique: tous les harmoniques sont présents avec même amplitude.

Expérimentalement, on lance un pendule de Mach en tournoiement : les frottements faibles feront transiter d'un mode à l'autre. La projection de la boule sur l'axe portant , elle, ne manifestera pas de transition : il y a continuité du phénomène.

Étude approfondie du spectre

Le développement en série de Fourier des fonctions de Jacobi sn, cn et dn sont connues. On en déduit un développement en série de Fourier de la vitesse angulaire.

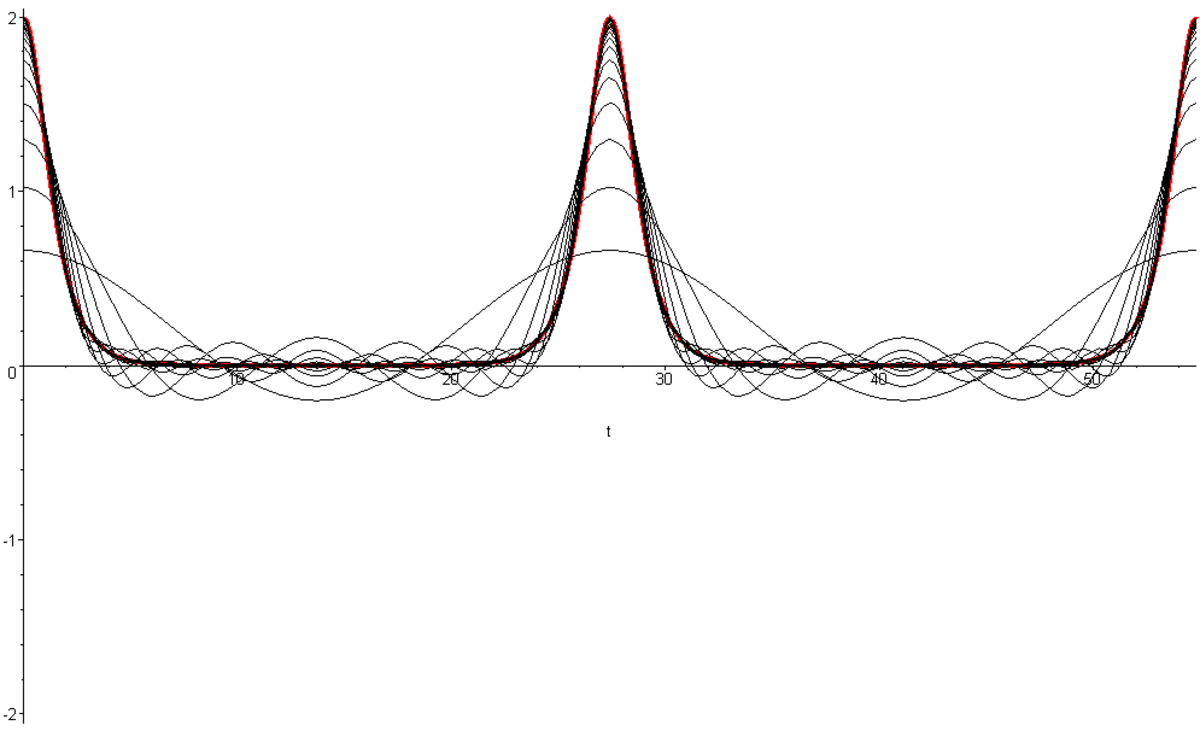
Cas k > 1 : soit N = T/To, avec T la période pour effectuer deux tours, correspondant à une rotation de 4π. N vaut . Nous prendrons comme pulsation fondamentale du mouvement . On a :

avec , et 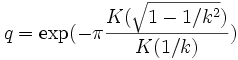. Si k est très grand, le mouvement est un mouvement de rotation autour de O à très grande vitesse. q est très petit, et le mouvement s'effectue quasiment selon la loi . Quand k diminue, q augmente, de sorte que les a_2n prennent de l'importance. Lorsque k est très légèrement supérieur à 1, N est très grand, et est très proche de 1. Le spectre est très étendu, puisque, pour n ~ N, a_n vaut encore environ 0,17.

Ci-dessous, les spectres de fréquence, par valeurs décroissantes de k, depuis une grande valeur jusqu'à une valeur légèrement supérieure à 1. En abscisse, on a porté les indices pairs 2n et en ordonnées les valeurs de a_2n (on a pris a₀ = 2) :

Grande valeur de k

Valeur intermédiaire

Valeur légèrement supérieure à 1

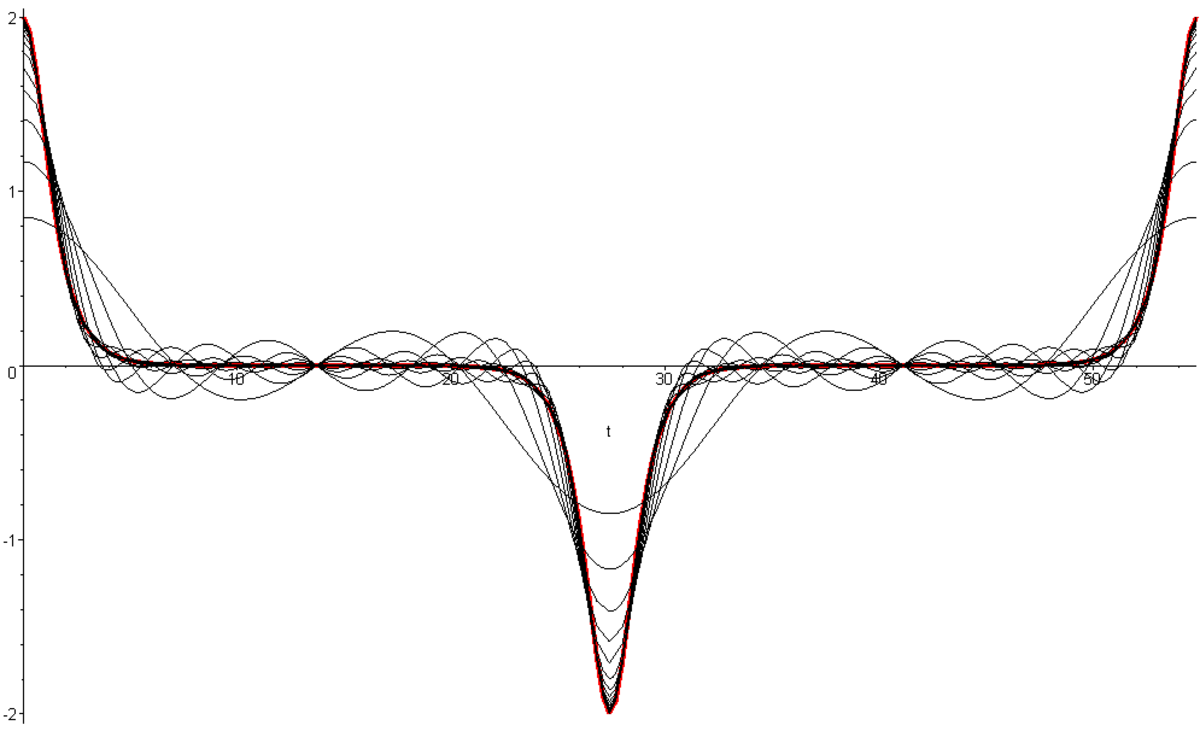
Cas k < 1 : la valeur de N est cette fois . La pulsation du mouvement est toujours . On a :

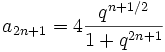avec , et 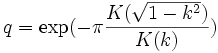. La situation où k est très légèrement inférieur à 1 est comparable à celle où k est très légèrement supérieur à 1. Lorsque k diminue, q décroît, et lorsque k est proche de 0, la pulsation prépondérante est celle qui correspond à ω.

Ci-dessous, les spectres de fréquence, par valeurs décroissantes de k, depuis une valeur légèrement inférieure à 1 jusqu'à une valeur très petite. En abscisse, on a porté les indices impairs 2n+1 et en ordonnées les valeurs de a_2n+1 :

Valeur légèrement inférieure à 1

Valeur intermédiaire

Très petite valeur de k

Voici également la représentation graphique de et la représentation des sommes partielles de Fourier correspondantes, d'une part pour k inférieur à 1, d'autre part pour k supérieur à 1 :

Série de Fourier du pendule simple

k < 1

k > 1