Paramagnétisme - Définition
La liste des auteurs de cet article est disponible ici.
Aspect macroscopique
Régime linéaire
Pour la plupart des matériaux dits paramagnétiques et sous des conditions raisonnables de température et de champ magnétique extérieur, l'aimantation
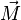
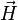
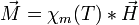
L'aimantation décroit avec température car celle-ci est le reflet macroscopique de l'agitation thermique des atomes. À noter que χm est en toute rigueur une matrice 3*3 mais se réduit dans la majorité des cas à un nombre scalaire dans le cas des matériaux lhi (linéaire, homogène et isotrope).
Régime saturé
Si le champ d'excitation augmente,
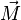
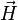
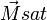
 , on parle alors de saturation.
, on parle alors de saturation.
Ce régime n'est pas observable à température ambiante car la susceptibilité magnétique y étant trop faible, il faudrait un
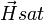
Ce régime est observable aux basses températures, de l'ordre de quelques Kelvin, à partir de champs de 0,5 à 1 Tesla.
Matériaux paramagnétiques
| Material | χm x 10-5 |
|---|---|
| Tungstène | 6.8 |
| Cesium | 5.1 |
| Aluminium | 2.2 |
| Lithium | 1.4 |
| Magnesium | 1.2 |
| Sodium | 0.72 |
- Aluminium Al [13] (métal)
- Baryum Ba [56] (métal alcalino-terreux)
- Calcium Ca [20] (métal alcalino-terreux)
- Oxygène liquide O2 [8] (non métallique)
- Platine Pt [78] (métal de transition)
- Sodium Na [11] (métal alcalin)
- Strontium Sr [38] (métal alcalino-terreux)
- Uranium U [92] (métal (actinide))
- Magnésium Mg [12] (métal alcalino-terreux)
- Fer γ (austénite) Fe [26]
- Technétium Tc [43] (métal de transition artificiel)
- Lithium Li [3] (métal alcalin)
Moment magnétique des électrons de conduction : paramagnétisme de Pauli
Dans un métal les électrons de conduction peuvent se déplacer presque librement, ils sont très faiblement liées aux atomes du métal (par exemple Modèle de Drude). Comme les électrons possèdent un moment magnétique de spin, on attend alors un apport à la susceptibilité, qui est similaire à la loi de Curie. Les électrons étant des fermions, ils doivent alors vérifier le principe de Pauli, et on observe la loi suivante :
-
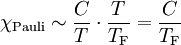
où TF est une constante du matériaux.
Pour être plus précis, on peut démontrer qu'il existe une dépendance de la force du champ magnétique.

















































