Parallélisme (informatique) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En informatique, le parallélisme consiste à implémenter des architectures d'électroniques numériques et les algorithmes spécialisés pour celles-ci, permettant de traiter des informations de manière simultanées. Le but de ces techniques est d'effectuer, par une machine, le plus grand nombre d'opération dans le plus petit temps donnés. Pour ce faire, les opérations doivent être faites en parallèle, c'est-à-dire simultanément au sein de plusieurs unités de traitement. Pour ce faire, la tâche à effectuer est décomposée en de multiples sous-tâches qui sont exécutées en même temps et qui composent chacune des architectures parallèles. Le parallélisme en informatique, comme défini ici, s'applique à de multiple type de traitement, mais sans spécification il s'agit de paralléliser les unités de calcul. Dans les autres cas comme pour le standard RAID 0, le terme d'agrégation est privilégié.
Pour être efficace, les méthodes utilisées pour la programmation des différentes tâches qui constituent un programme sont spécifiques à ce mode de calcul, c'est-à-dire que les programmes doivent être réalisés avec cette optique. Ces méthodes ont initialement été développées sur des machines sophistiquées, des superordinateurs qui comptent de nombreux processeurs.
Par ailleurs, les architectures parallèles sont devenues le paradigme dominant pour tous les ordinateurs depuis les années 2000. En effet, la vitesse de traitement qui est liée à l'augmentation de la fréquence des processeurs connait des limites en raison d'une augmentation de la production thermique qui provoque des erreurs de calculs. C'est aussi la raison pour laquelle depuis longtemps déjà l'augmentation de la vitesse de calcul passait par une architecture comportant de nombreuses unités de calcul. La création de processeurs multi-cœurs, traitant plusieurs instructions en même temps au sein du même composant, résout ce dilemme pour les machines de bureau depuis le milieu des années 2000. Parallèlement à ce phénomène, les développeurs de logiciels utilisent plus volontiers sur ces machines, le type de programmation spécialisé appelée programmation concurrente qui est souvent plus efficace mais plus compliquée à mettre en place que la programmation traditionnelle dite séquentielle.
Les ordinateurs parallèles peuvent être grossièrement classées selon le niveau auquel le matériel prend en charge le parallélisme. D'une part, il y a les machines communes que ce soit avec multi-cœurs ou les machines multiprocesseurs et d'autre part les architectures en grappe de serveurs, les machines massivement parallèles et les structures formées à partir de grilles informatiques c'est-à-dire de milliers de simples ordinateurs, non dévolus à cette tâche en particulier, et reliés par un simple réseau.
Principes
Les premiers ordinateurs étaient séquentiels, c'est-à-dire que leur processeur n'exécutait les instructions que l'une après l'autre, passant éventuellement d'un processus à un autre via des interruptions en simulant le multitâche. Les machines parallèles exécutant des programmes parallélisés ne se contentent pas d'effectuer des applications indépendantes en parallèle. Le système d'exploitation, via son ordonnanceur, ou l'intergiciel doit répartir les calculs de manière à optimiser l'utilisation des unités de calcul. C'est un problème général en informatique connu sous le nom répartition de charge. Pour que ce soit efficace, il faut que les applications soient écrites de telle façon que les algorithmes soient constitués de tâches, c'est-à-dire écrit par « tranches » dont les exécutions pourront se faire de manière relativement indépendantes les unes des autres sur les différentes unités de calcul. Pour que ceci soit possible le programme doit être écrit suivant le paradigme de la programmation concurrente, une méthode de programmation utilisant des mécanismes formalisés. Ceci accélère le traitement dans la plupart des situations même si certaines tâches doivent attendre la résolution d'une autre, concurrente sur une ressource par exemple, pour continuer à s'effectuer.
Il s'avère dans la pratique que la multiplication du nombre d'unités de calcul ne divise pas spontanément le temps d'exécution des programmes, même lorsque le programme utilise les mécanismes de la programmation concurrente. De nombreuses autres considérations entrent en jeu comme la perte de temps pour l'attente de données calculées par une autre tâche. Concrètement, deux soucis se posent lorsqu'un centre informatique choisit d'utiliser cette méthode de calcul. Éviter d'utiliser une machine trop puissante, car cela a un coût, et écrire le meilleur programme qui soit. Techniquement, les limites de puissance de calcul sont indissociables des problèmes de dispersion thermique des processeurs.
La réalisation de programmes adéquats sur des architectures prévues à cet effet se traduit par des économies dans presque tous les domaines du calcul, incluant : la dynamique des fluides, les prédictions météorologique, la modélisation et simulation de problèmes de dimensions plus grandes, le traitement de l'information et l'exploration de données, le traitement d'images ou la fabrication d'images de synthèse, tels que le lancer de rayon, (avec les fermes de rendu), l'intelligence artificielle et la fabrication automatisée. En fait, la plupart des systèmes de calcul de haute performance (aussi appelés superordinateurs ou supercalculateurs) qui ont été conçus au cours des dernières années ont une architecture parallèle.
Elle permet aussi de traiter des problèmes nouveaux, d'apporter des solutions globales à des problèmes qui étaient abordés plus partiellement auparavant.
La taxinomie de Flynn
| Unique instruction | Multiple instructions | |
|---|---|---|
| Donnée unique | SISD | MISD |
| Plusieurs données | SIMD | MIMD |
La Taxinomie de Flynn, proposée par l'américain Michael J. Flynn est l'un des premiers systèmes de classification des ordinateurs créé, il évalue tant le matériel que le logiciel. Les programmes et les architectures sont classés selon le type d'organisation du flux de données et du flux d'instructions. Les machines les plus simples traitent une données à la fois et en même temps, ces systèmes SISD sont dit « séquentielles ». Ce type de fonctionnement était prédominent pour les ordinateurs personnels jusqu'à la fin des années 1990. Le type MISD a été beaucoup plus rarement utilisé, il semble néanmoins adapté à certains problèmes comme les réseaux neuronaux et aux problèmes temps-réel liés. L'architecture appelée Systolic array est un type d'architecture MISD. Les systèmes traitants de grandes quantités de données d'une manière uniforme ont intérêt à être des SIMD, c'est typiquement le cas des processeurs vectoriels ou des unités de calcul gérant le traitement du signal comme la vidéo ou le son, c'est par exemple le cas des machines traitant les instructions AltiVec. Les systèmes utilisant plusieurs processeurs ou un processeurs multi-cœurs sont plus polyvalents et pleinement parallèle, ce sont des MIMD.
Selon David A. Patterson et John L. Hennessy, « Certaines machines sont des hybrides de ces catégories, bien sûr, mais cette classification traditionnelle a survécu parce qu'elle est simple, facile à comprendre, et donne une bonne première approximation. C'est aussi, peut-être en raison de son intelligibilité, le schéma le plus utilisé. »
Cette approche montre clairement deux types de parallélismes différents, le parallélisme par flot d'instructions également nommé parallélisme de traitements ou de contrôle, dans l'optique d'opérations simultanées et le parallélisme de données en multipliant le même traitement sur un grand nombre de données.
Efficacité du parallélisme
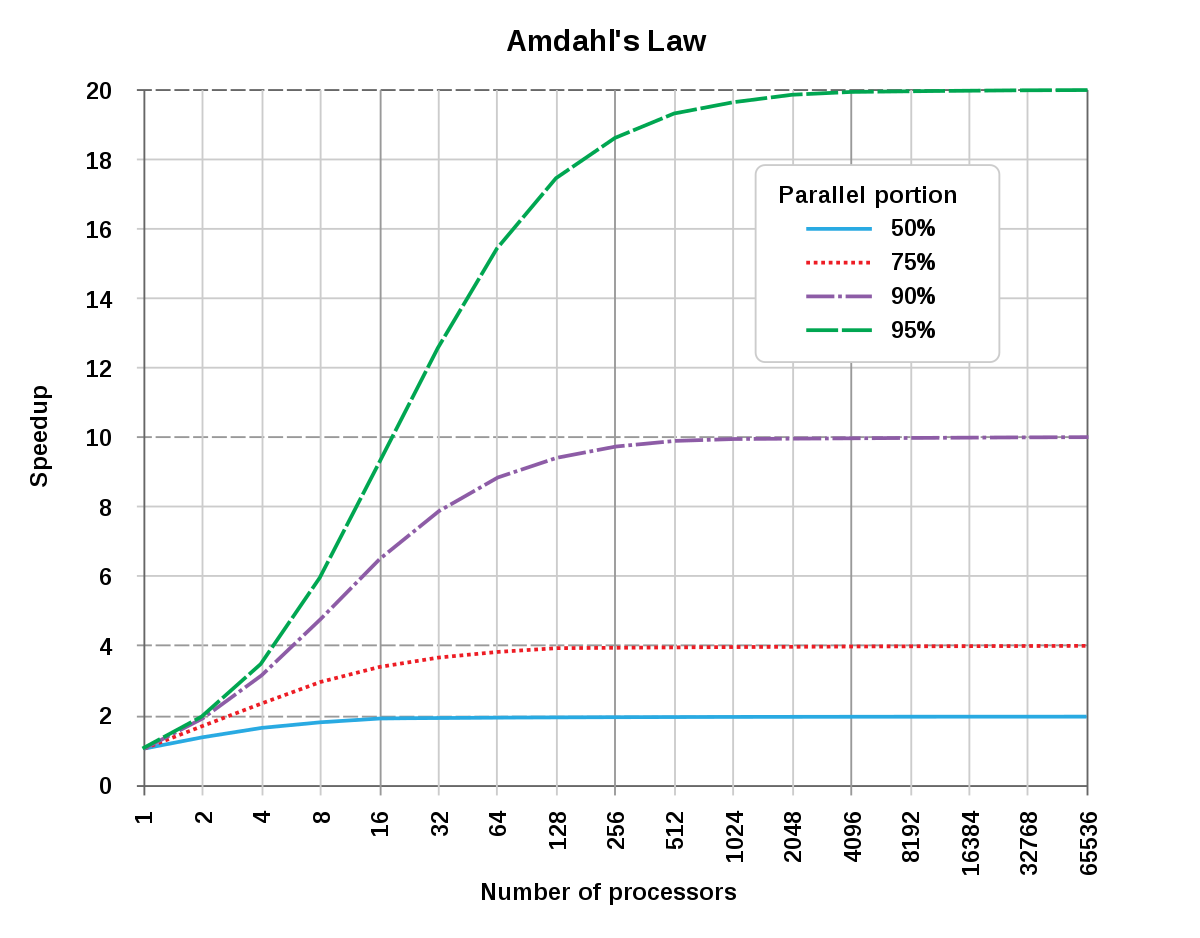
De façon idéale, l'accélération due à la parallélisation devrait être linéaire, en doublant le nombre d'unités de calcul, on devrait réduire de moitié le temps d'exécution, et ainsi de suite. Malheureusement très peu de programmes peuvent prétendre à de telles performances. Dans les années 1960, Gene Amdahl formula une loi empirique éponyme restée célèbre, elle aussi fut développée par d'autres auteurs. La loi d'Amdahl affirme que la petite partie du programme qui ne peut être parallélisée limite la vitesse globale du programme. Or tous les programmes d'ingénierie ou toute résolution mathématique contient nécessairement des parties parallélisables et des parties séquentielles non parallélisables. Cette loi prévoit, qu'une fois optimisé, il existe au sein du programme une relation entre ration de code parallélisé et la vitesse globale d'exécution du programme. Dans la pratique, cette approximation est utilisée pour fixer une limite à la parallélisation des architectures matérielles ou à l'optimisation de la programmation pour résoudre un problème.
La loi de Gustafson est assez analogue. Également empirique, elle prédit que le gain de vitesse obtenu est proportionnel à la fois au taux que représente la partie non-parallélisable et au nombre de processeurs.
La métrique de Karp-Flatt proposée en 1990 est plus complexe et efficace que les deux autres lois. Elle intègre le coût lié au temps d'exécutions des instructions qui mettent en œuvre le parallélisme.
Autres considérations empiriques
Une autre thèse veut que tout problème pouvant être résolu sur un ordinateur séquentiel raisonnable en utilisant un espace de taille polynomiale peut être résolu en temps polynomial par un ordinateur parallèle raisonnable et vice versa.
La thèse de l'invariance est une thèse complémentaire qui supporte, du moins de façon approximative, la définition d'une notion d'ordinateur raisonnable. Elle s'énonce comme suit: Des machines raisonnables peuvent se simuler entre elles avec au plus un accroissement polynomial en temps et une multiplication constante de l'espace. Une manière de construire des modèles « raisonnables » est de considérer la classe des machines raisonnables incluant la machine de Turing.
Depuis les années 1960, la densité des transistors dans un microprocesseur double tous les 18 à 24 mois, cette observation est appelée la loi de Moore. En dépit de problèmes de consommation énergétique, la loi de Moore est toujours valable en 2010. Les transistors supplémentaires, toujours plus petits, permettent de créer plusieurs unités de calcul, appelé cœurs, au sein du même processeur.


















































