Orthogonalité - Définition

Dimension finie

Espace euclidien

Un espace euclidien E est un espace vectoriel réel de dimension finie, ici noté n et muni d'un produit scalaire (.|.). Au lieu de point, on parle en général de vecteur. La distance d entre deux vecteurs x et y est donnée par la formule suivante :

Si Φ est une partie de E, alors l'orthogonal de Φ est un sous-espace vectoriel de E et plus précisément :

Cette proposition est une conséquence des propriétés sur l'orthogonalité démontrées dans l'article Forme bilinéaire. Cette propriété apporte un intérêt à la notion de projecteur parallèlement à son orthogonal. Une telle application est nommée projection orthogonale. On en déduit aussi que l'orthogonal du vecteur nul est l'espace entier et l'orthogonal de l'espace entier est le vecteur nul.

Soient Φ₁ et Φ₂ deux parties parties de E, alors :

proposition 2 —  Les relations d'orthogonalités suivantes sont vérifiées, si Vect(A) désigne l'espace vectoriel engendré par une partie A de E :

Ces relations sont démontrées dans l'article Forme bilinéaire.

L'orthogonal d'un vecteur non nul est un hyperplan et tout sous-espace vectoriel F différent de E s'exprime comme intersection d'hyperplans. Plus précisément, tout sous-espace vectoriel de codimension p, si p est un entier strictement positif, est l'intersection de p hyperplans. Comme tout hyperplan s'exprime comme l'orthogonal d'un vecteur, la deuxième propriété de la proposition 2 indique donc l'existence de p vecteurs (v_i) pour i variant de 1 à p tel que :

Enfin, le procédé d'orthogonalisation de Gram-Schmidt montre l'existence d'une base orthogonale. Si (e_i), pour i variant de 1 à n, est une base orthogonale, alors tout vecteur x de E s'exprime comme une combinaison linéaire de la base à l'aide du produit scalaire et la norme de x comme une somme de carrés de produits scalaire de x avec les éléments de la base :

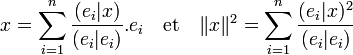
Ces propriétés se déduisent de celles démontrées dans l'article Inégalité de Bessel. Il traite aussi du cas où la famille n'est pas génératrice.

Espace hermitien

Charles Hermite généralise l'approche euclidienne sur les espaces complexes qui portent maintenant son nom. Les conditions nécessaires et suffisantes d'orthogonalité précédentes ne s'appliquent plus. Si x et y sont deux vecteurs d'un espace hermitien H, on dispose de la relation suivante :

En revanche, toutes les propriétés décrites dans le paragraphe Espace euclidien restent valables.

Forme bilinéaire symétrique

Dans le cas d'une forme bilinéaire symétrique (.|.), il peut exister un sous-espace vectoriel orthogonal à l'espace entier E.

L'orthogonal du vecteur nul est l'espace entier et l'orthogonal de l'espace entier est le noyau. De plus, tout orthogonal d'une famille Φ contient le noyau. Soit N le noyau de la forme (.|.) et M un supplémentaire du noyau dans E. La restriction de (.|.) à M est non dégénérée. Sur cette restriction, les propositions 1 et 2 du paragraphe Espace euclidien restent valides. Ces résultats sont démontrés dans l'article Forme bilinéaire.

La réduction de Gauss montre l'existence de base orthogonal pour (.|.). Cette réduction s'applique aux formes quadratiques, cependant réduire une forme quadratique, c'est-à-dire trouver une base orthogonale pour cette forme quadratique revient à trouver une base orthogonale pour sa forme polaire. Sylvester va plus loin dans son analyse. Sa loi stipule qu'il existe un couple d'entier (q, r) tel que, pour toute base orthogonale (e_i), L'expression (e_i | e_i) est strictement positive exactement q fois, strictement négative exactement r et que le noyau de la forme bilinéaire est de dimension n - q - r. Ici n désigne la dimension de E.

Le théorème de Weierstrass montre comment s'expriment les relations d'orthogonalités si deux formes bilinéaires symétriques dont l'une est définie positive sont en présence :

Ce théorème est démontré dans l'article Endomorphisme autoadjoint. Il existe un équivalent de forme bilinéaire symétrique pour les espaces complexes, ce sont les formes sesquilinéaires. Tous les résultats de ce paragraphe s'appliquent aussi à ces formes.

Cas général

Si la forme bilinéaire n'est pas symétrique, il existe encore un cas où il est possible de parler d'orthogonalité au sens précédent, celui des formes réflexives.

Définition —  La forme bilinéaire est dite réflexive si et seulement si la propriété suivante est vérifiée:

La configuration est alors la même que celle de la forme bilinéaire symétrique. Sur un supplémentaire du noyau, la forme est non dégénérée et les propositions 1 et 2 du paragraphe sur les espaces euclidiens s'appliquent. Dans le cas général l'orthogonal du vecteur nul est l'espace entier et l'orthogonal de l'espace entier est le noyau. Enfin, tous les orthogonaux contiennent le noyau.

Dans le cas général, il devient nécessaire de parler d'orthogonalité à gauche et à droite. Soit Φ une famille de vecteur, l'orthogonal à gauche de Φ est défini par l'ensemble suivant :

Si la forme bilinéaire est définie sur un produit ExF de deux espaces vectoriel, alors l'ambigüité n'existe pas. L'orthogonal d'une famille d'éléments de E est un sous-espace vectoriel de F et réciproquement.

La codimension des noyaux à droite et à gauche sont les mêmes. Si M₁ (resp. M₂) est un supplémentaire du noyau à gauche N₁ (resp. à droite N₂), alors tout vecteur x (resp. y) de l'espace de gauche (resp. de droite) s'exprime de manière unique comme somme d'un vecteur x₁ (resp. y₁) du supplémentaire du noyau et d'un vecteur du noyau. La restriction de la forme bilinéaire à M₁xM₂ est non dégénérée et :

Plus de détails sur les orthogonaux dans cette configuration sont donnés dans l'article Forme bilinéaire.