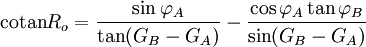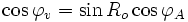Orthodromie - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Formule de l'orthodromie
Voici le résultat du calcul de l'orthodromie entre A
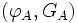
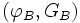
- distance orthodromique M :
- gain (m-M) en distance par rapport à la loxodromie :
-
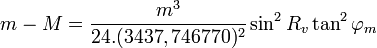
- avec :
-
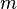
-

-
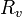
-
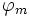
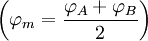
-
- route initiale
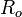
- latitude du vertex
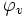
![M = 60\arccos \,[\sin \varphi_A\sin \varphi_B + \cos \varphi_A\cos \varphi_B \cos (G_B - G_A)]\,](https://static.techno-science.net/illustration/Definitions/autres/3/3fad30bc991daf184c22cc82f1d86071_382c8230b38086644a80efed0e00e9a8.png)