Orientation (mathématiques) - Définition

Orientation d'un espace affine

L'orientation d'une droite affine dépend du choix d'un vecteur directeur, ou plutot du choix d'un tel vecteur à positive colinéarité près. Le choix d'une orientation pour un espace affine de dimension finie doit donc dépendre du choix d'un repère ; mais l'origine doit jouer un role secondaire dans la définition. L'orientation est donc imposée par le choix d'une base de l'espace directeur.

Deux bases d'un espace vectoriel réel E définissent la même orientation lorsque le déterminant de la matrice de passage est (strictement) positif. Cette matrice est évidemment inversible : son déterminant est donc non nul. Est ainsi définie une relation d'équivalence sur l'ensemble des bases de E, relation admettant exactement deux classes d'équivalence, les orientations de E. Une fois fixée une orientation, une base de E est dite base directe ou base indirecte selon que cette base définit l'orientation choisie ou l'autre. Une orientation d'un espace affine est une orientation de l'espace directeur. Le vocabulaire correspondant est repère direct ou repère indirect.

L'espace Rⁿ admet une base canonique, et donc une orientation canonique.

Cette définition généralise fort heureusement la situation en dimension 1.

Orientation d'un plan

Pour un plan vectoriel P, le choix d'une orientation est imposé par le choix de deux vecteurs non colinéaires, formant donc une base . Intuitivement, l'orientation d'un plan consiste à définir la manière de tourner autour d'un point. On tourne autour de 0 en parcourant une courbe enfermant 0, en allant de en direction de et en retournant à sans faire demi-tour. Il n'est donc pas étonnant à ce que la question de l'orientation soit lié au problème des angles orientés en géométrie euclidienne.

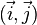
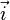
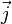
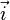
L'orientation d'un plan vectoriel euclidien E se résume essentiellement au choix d'une orientation de son cercle unité. Cette orientation revient à fixer un signe au niveau des mesures d'angle.

Par le théorème de Jordan, une courbe de Jordan, c'est-à-dire une courbe périodique et simple (injective sur une période), d'un plan orienté P borde un domaine compact du plan P (voir figure). Il existe donc une notion naturelle d'intérieur et d'extérieur. On impose à un paramétrage c que pour tout vecteur sortant n(t) en c(t), (c '(t), n(t)) soit une base directe. Ainsi, toute courbe de Jordan d'un plan orienté est naturellement orientée.

Orientation de l'espace de dimension trois

Orienter l'espace consiste également à choisir une base directe arbitraire. On respecte généralement la règle des trois doigts de la main droite. Un plan et une droite perpendiculaires peuvent être orientés corrélativement. Les règles du bonhomme d'Ampère et du tire-bouchon de Maxwell sont utilisés par les physiciens pour expliquer intuitivement ce que signifie orienter l'espace.

Si cette convention est choisie, alors on a concrètement :

• Le sens direct de l'espace correspond au mouvement d'une vis que l'on visse dans une plaque de bois ;
• Son sens indirect correspondant alors au mouvement de la vis que l'on dévisse de cette plaque de bois.

L'orientation d'un espace vectoriel euclidien de dimension 3 autorise l'introduction du produit vectoriel. L'orientation intervient dans le choix du sens du vecteur .

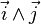
Espace vectoriel complexe

Un espace vectoriel complexe E de dimension finie est, en tant qu'espace vectoriel réel, naturellement orienté. Plus exactement, si e=(e₁,...,e_n) est une base complexe de E, alors e' = (e₁,e₂,...,e_n,i.e₁,i.e₂,...,i.e_n) est une base vectorielle réelle de E. Si M est la matrice de passage entre deux bases complexes e et f, alors la matrice de passage entre les bases complexes correspondantes est :

.

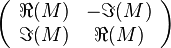
Son déterminant est | det(M) | ². Etant positif, les bases e' et f' définissent les mêmes orientations de E.