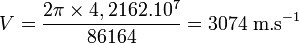Orbite géostationnaire - Définition

Calcul de l'altitude de l'orbite géostationnaire

• La seconde loi de Newton donne :
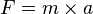
• Le mouvement étant circulaire uniforme on a:
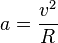
• Loi de la gravitation universelle énonce :

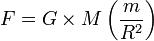
avec :

• G est la constante de la gravitation universelle
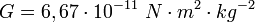
• M_T est la masse de la Terre
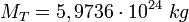
• m_s est la masse du satellite
• R_T est le rayon de la Terre à l'équateur
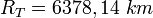
• h est l'altitude du satellite
• R = R_T + h
• v est la vitesse linéaire du satellite

d'où

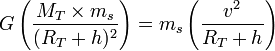
La vitesse, pour une trajectoire circulaire est :

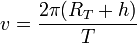
où T est la période du mouvement, c’est-à-dire le temps que doit mettre le satellite pour faire un tour autour de la Terre.

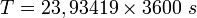
Après calcul on obtient :

soit

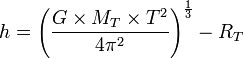
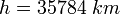
Rejoindre l'orbite géostationnaire

Le placement d'un satellite en orbite géostationnaire est une opération complexe qui peut prendre plusieurs semaines.

Au départ, le satellite est sur une orbite de transfert géostationnaire.

Orbite cimetière

Lorsqu'un satellite en orbite géostationnaire arrive en fin de vie, généralement par épuisement de ses ergols, il ne peut plus être contrôlé pour rester rigoureusement géostationnaire. On le fait alors dériver vers une orbite très proche, dite « orbite cimetière » où il va rester, comme débris spatial pour une durée indéterminée.

Il est généralement demandé aux contrôleurs de satellites d'utiliser les quelques derniers kilogrammes d'ergols restant (si le satellite est toujours manœuvrable) pour repositionner le satellite un peu plus loin que l'orbite géostationnaire, lui évitant de passer ensuite proche des autres satellites en activité. Ensuite, il est demandé de couper tous les circuits électriques, évitant qu'il n'interfère avec les autres satellites près desquels il va passer, ainsi que de vider complètement les réservoirs d'ergols afin de se prémunir d'une explosion suite à une éventuelle collision avec un autre objet céleste.

Cette orbite présente un point d'anomalie où ont tendance à s'accumuler les satellites morts : proche du méridien 75 ° est, où se manifeste une modification du potentiel géogravitationnel terrestre, dû probablement à la présence du massif Himalayen.

Calcul de la vitesse du satellite

À partir de la seconde loi de Newton et de la loi de la gravitation universelle on peut écrire :

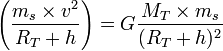
d'où

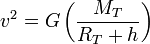
Pour on obtient :

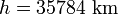
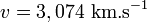
Autre méthode de calcul :

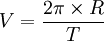
où R est la distance du centre de la Terre au satellite (en mètres), soit :

R = R_t + h : rayon de la Terre R_t + altitude du satellite h

et T est la période des satellites géostationnaires soit 86 164 s