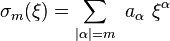Opérateur différentiel - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Notations - Transformée de Fourier - Définition d'un opérateur différentiel - Exemples importants pour la physique théorique - Classification des opérateurs différentiels - Cas général - Opérateur différentiel à coefficients constants

Définition d'un opérateur différentiel

Définition

Un opérateur différentiel linéaire d'ordre $m$ est défini par :

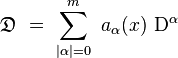
où les $a α (x)$ sont des fonctions de $n$ variables, appelées coefficents de l'opérateur $\mathfrak{D}$ .

Propriété de localité

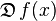
Un opérateur différentiel $\mathfrak{D}$ est local au sens où, pour déterminer ses effets $\mathfrak{D} \, f(x)$ sur une fonction $f (x)$ suffisamment différentiable, seule la connaissance de la fonction dans le voisinage du point $x$ est nécessaire.

Exemples importants pour la physique théorique

La physique théorique fait un usage abondant de trois opérateurs d'ordre 2 :

Opérateur laplacien

L'opérateur laplacien est un opérateur elliptique, qui s'écrit :

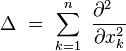
en coordonnées cartésiennes dans $\R^n$ : $\Delta \ = \ \sum_{k=1}^n \ \frac{\partial^2 ~~}{\partial x_k^2}$

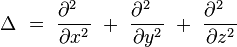
soit en coordonnées cartésiennes tridimensionnelles : $\Delta \ = \ \frac{\partial^2 ~~}{\partial x^2} \ + \ \frac{\partial^2 ~~}{\partial y^2} \ + \ \frac{\partial^2 ~~}{\partial z^2}$

Cet opérateur est notamment utilisé en mécanique newtonienne, en électromagnétisme, et en mécanique quantique non relativiste.

Opérateur d'alembertien

L'opérateur d'alembertien est un opérateur hyperbolique, qui s'écrit en coordonnées cartésiennes $(x, t)$ dans $\R^{n+1}$ :

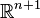
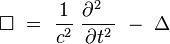
où $Δ$ est le laplacien à $n$ variables d'espace, $t$ est le temps, et $c$ une constante positive, homogène à une vitesse. Cet opérateur est utilisé pour décrire la propagation des ondes à la vitesse $c$ dans l'espace-temps. Il est notamment utilisé en acoustique, en électromagnétisme, et en théorie quantique des champs.

Opérateur de la chaleur

L'opérateur de la chaleur, qui s'écrit en coordonnées cartésiennes $(x, t)$ dans $\R^{n+1}$ :

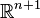
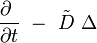
où $Δ$ est le laplacien à $n$ variables d'espace, $t$ est le temps, et $\tilde{D}$ est ici une constante, appelée coefficient de diffusion. Cet opérateur est dit parabolique.

Classification des opérateurs différentiels

Opérateur elliptique

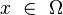
L'opérateur différentiel $\mathfrak{D}$ est dit elliptique au point $x \ \in \ \Omega$ si et seulement si :

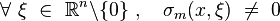
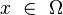
$\mathfrak{D}$ est dit elliptique dans $Ω$ s'il est elliptique pour tout point $x \ \in \ \Omega$ .

Opérateur hyperbolique

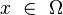
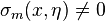
L'opérateur différentiel $\mathfrak{D}$ est dit hyperbolique dans la direction $η$ au point $x \ \in \ \Omega$ si et seulement si : $\sigma_m (x, \eta) \ne 0$ et si, pout tout $ξ$ non colinéaire à $η$ , les racines $λ i$ de l'équation :

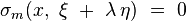
sont toutes réelles. Si, de plus, les $m$ racines réelles sont toutes distinctes, l'opérateur $\mathfrak{D}$ est dit strictement hyperbolique dans la direction $η$ .

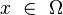
$\mathfrak{D}$ est dit (strictement) hyperbolique dans la direction $η$ dans $Ω$ s'il est strictement hyperbolique dans la direction $η$ pour tout point $x \ \in \ \Omega$ .

Cas général

On a vu que plus haut :

$(\mathfrak{D} \,f)(x) \ = \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, \xi \, , \, x \, >} \ \sigma (x,\xi) \ \hat{f}(\xi)$

Pour un opérateur différentiel dont les coefficients $a α (x)$ ne sont pas constants, le symbole $σ(x,ξ)$ dépend des coordonnées d'espace $x$ , et on a :

Expression de la transformée de Fourier

Partons de la relation générale :

$(\mathfrak{D} \,f)(x) \ = \ \sum_{|\alpha| = 0}^m \ a_{\alpha}(x) \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, \xi \, , \, x \, >} \ \xi^{\alpha} \ \hat{f}(\xi)$

Si l'on introduit la transformée de Fourier des coefficients :

$a_{\alpha}(x) \ = \ \int_{\mathbb{R}^n} \mathrm d \tilde{\eta} \ e^{+ \, i \, < \, \eta \, , \, x \, >} \ \hat{a}_{\alpha}(\eta)$

on obtient :

$(\mathfrak{D} \,f)(x) \ = \ \sum_{|\alpha| = 0}^m \ \int_{\mathbb{R}^n} \mathrm d \tilde{\eta} \ e^{+ \, i \, < \, \eta \, , \, x \, >} \ \hat{a}_{\alpha}(\eta) \ \times \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, \xi \, , \, x \, >} \ \xi^{\alpha} \ \hat{f}(\xi)$

soit :

$(\mathfrak{D} \,f)(x) \ = \ \sum_{|\alpha| = 0}^m \ \int_{\mathbb{R}^n} \mathrm d \tilde{\eta} \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ e^{+ \, i \, < \, (\xi + \eta ) \, , \, x \, >} \ \hat{a}_{\alpha}(\eta) \ \xi^{\alpha} \ \hat{f}(\xi)$

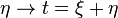
A $ξ$ fixé, on fait le changement de variable : $\eta \to t = \xi + \eta$ , ce qui donne :

$(\mathfrak{D} \,f)(x) \ = \ \sum_{|\alpha| = 0}^m \ \int_{\mathbb{R}^n} \mathrm d \tilde{t} \ e^{+ \, i \, < \, t \, , \, x \, >} \ \int_{\mathbb{R}^n} \mathrm d \tilde{\xi} \ \hat{a}_{\alpha}(t - \xi) \ \xi^{\alpha} \ \hat{f}(\xi)$

On reconnait le produit de convolution :

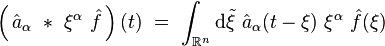
d'où :

$(\mathfrak{D} \,f)(x) \ = \ \sum_{|\alpha| = 0}^m \ \int_{\mathbb{R}^n} \mathrm d \tilde{t} \ e^{+ \, i \, < \, t \, , \, x \, >} \ \left( \, \hat{a}_{\alpha} \ * \ \xi^{\alpha} \ \hat{f} \, \right)(t)$

qu'on peut réécrire :

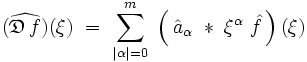
Opérateur différentiel à coefficients constants

Si les coefficients $a α$ sont indépendants des $n$ variables d'espace $x k$ , le symbole de l'opérateur différentiel $\mathfrak{D}$ d'ordre $m$ est seulement une fonction $σ(ξ)$ des $n$ variables $ξ$ polynomiale en $ξ$ :

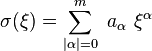
de telle sorte que :

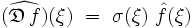
Le symbole principal de l'opérateur différentiel $\mathfrak{D}$ d'ordre $m$ à coefficients constants est la fonction des $n$ variables $ξ$ :

Transformée de Fourier

Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁

L'électroluminescence du graphène, une découverte inattendue ! 💡

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

Page générée en 0.103 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise