Notations delta en sciences - Définition

δ (delta minuscule)

Une variation peut s'étudier comme résultant de l'accumulation successive de plusieurs petits apports. Chacun de ces apports n'est pas considéré comme une variation à proprement parler, mais comme une quantité élémentaire. On utilise la lettre grecque delta minuscule δ pour indiquer une telle petite quantité n'étant pas une variation. Cependant la variation (Δ, d ou ) d'une grandeur peut dépendre de cet apport δ.

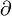
Par exemple, considérons un compte bancaire en euros sur lequel sont effectués plusieurs petits prélèvements P d'argent (petits par rapport au total de tout ce qui sera prélevé). Si P vaut 10 euros, on peut noter cette quantité δP = 10. Cette quantité est simplement une valeur numérique qui ne correspond pas à un écart entre deux sommes d'argents, ou à un gain ou une perte. Le compte subit maintenant une variation de valeur − δP (retrait de la quantité numérique 10 euros), si bien qu'on peut maintenant parler de la variation du montant total T du compte. Pour autant, le montant δP n'est pas, lui, une variation (un billet de 10 a la valeur qu'il a, c'est une quantité, pas une variation). Si on voyait les comptes (débité et destinataire) comme deux récipients reliés par un tuyau, on pourrait parler de la variation de niveau d'un des récipients. Mais on ne parlerait pas de variation de niveau d'eau dans le tuyau. L'eau y circule mais le tuyau est toujours plein. C'est aussi le cas de notre δP : c'est une quantité créée ou déplacée, pas une variation en tant que telle. L'introduction de la notation δ correspond donc essentiellement à un besoin de distinction sémantique entre variation et 'amplitude d'une variation.

On retrouve souvent cette distinction en physique. Par exemple, considérons le travail d'une force F sur un petit déplacement dL : on note δW un travail élémentaire sur un court déplacement et on a la relation — on fait généralement le bilan énergétique d'un système, dont on étudie par exemple l'évolution d'énergie interne. Ce travail élémentaire étant « hors système » δW n'est pas la variation d'une grandeur mais un prélèvement ou dépôt élémentaire d'énergie. C'est une manière de voir les choses, car on pourrait dans un autre contexte décider de s'intéresser à une fonction f représentant l'énergie totale apportée par le travail de cette force F : on noterait alors df comme précédemment. De façon générale, pour le travail d'une force, on n'écrit pas ΔW mais W : on ne le voit pas comme la variation d'une grandeur mais comme une quantité d'énergie. Et δW est donc un des apports élémentaires en cours de route, une partie de la quantité totale.