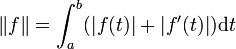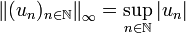Norme (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie, la norme est une extension de la valeur absolue des nombres aux vecteurs. Elle permet de mesurer la longueur commune à toutes les représentations d'un vecteur dans un espace affine, mais définit aussi une distance entre deux vecteurs invariante par translation et compatible avec la multiplication externe.
La norme usuelle dans le plan ou l'espace est dite euclidienne car elle est associée à un produit scalaire, à la base de la géométrie euclidienne.
D'autres normes sont très utilisées sur les espaces vectoriels de dimension finie ou infinie, appelés alors espaces vectoriels normés. Elles sont notamment très importantes en analyse fonctionnelle pour obtenir des majorations, exprimer la différentiation sur les espaces de fonctions d'une ou plusieurs variables réelles ou complexes, calculer estimations et approximations.
Il existe une deuxième définition de la norme, utilisé en arithmétique, elle est traitée dans l'article Norme (arithmétique).
Géométrie euclidienne usuelle
Définition
Si A et B sont deux points du plan ou de l'espace usuel, la norme du vecteur
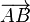
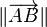
La norme, la direction et le sens sont les trois données qui caractérisent un vecteur et qui ne dépendent donc pas du choix du représentant.
Calcul
La norme d'un vecteur peut se calculer à l'aide de ses coordonnées dans un repère orthonormé à l'aide du théorème de Pythagore.
- Dans le plan, si le vecteur
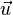
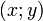
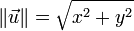
- Si les points A et B ont pour coordonnées respectives
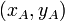
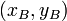
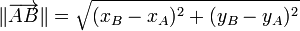
- Dans l'espace, si le vecteur
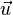
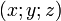
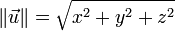
- Si les points A et B ont pour coordonnées respectives
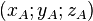
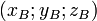
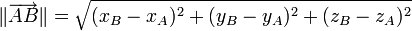
La norme d'un vecteur peut s'obtenir à partir du produit scalaire :
-
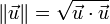
Réciproquement, le produit scalaire peut s'obtenir à partir de la norme grâce à la relation :
-
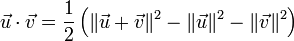
Propriétés
- La norme ne s'annule que pour le vecteur nul
- La norme du produit par un nombre est le produit de la norme par la valeur absolue de ce nombre :
-
-
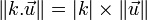
-
- En particulier, tout vecteur a la même norme que son opposé :
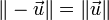
Exemples
En dimension finie
On considère le vecteur sur Kn,
- la norme euclidienne est obtenue à partir du produit scalaire ou du produit hermitien canoniques :
-
-
- et elle correspond à la norme habituellement utilisée pour la distance entre deux points dans le plan ou l'espace usuels (la présence du 2 en indice est expliquée juste après);
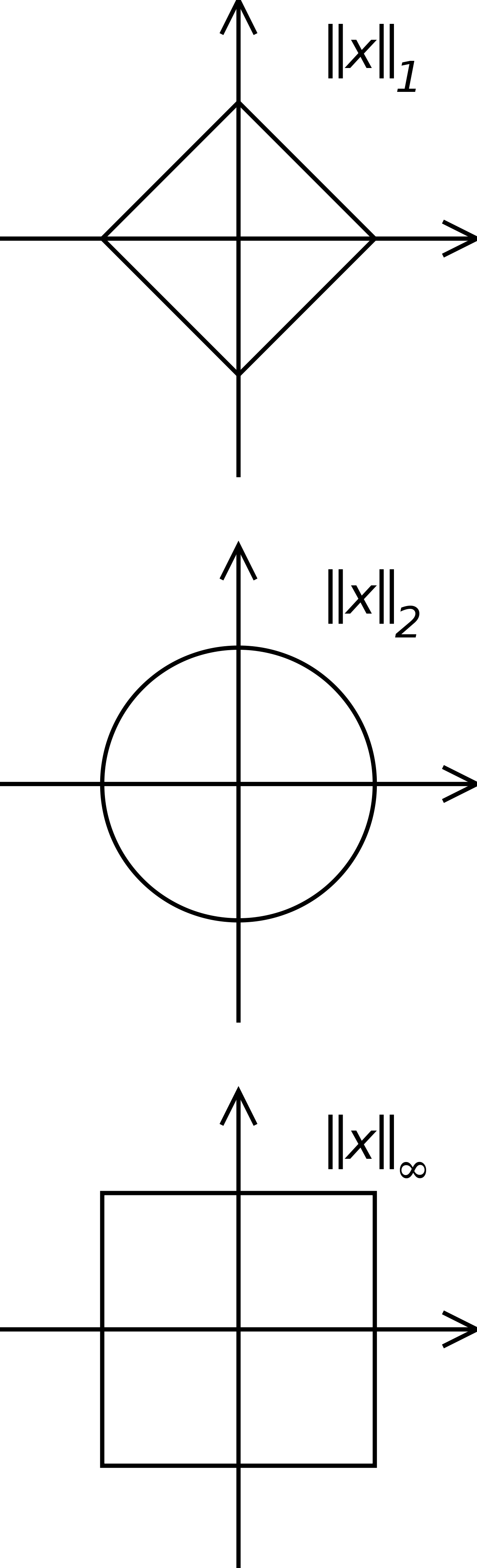
- la norme 1 est donnée par la somme des modules (ou valeurs absolues) des coefficients :
-
-
- et induit la distance de déplacement à angle droit sur un damier (ou dans les rues de Manhattan) ;
- plus généralement, pour tout p supérieur ou égal à 1, la norme p est donnée par la formule suivante :
-
-
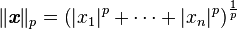
-
- elle identifie donc la norme euclidienne avec la norme 2, mais n'a surtout d'intérêt que dans sa généralisation aux espaces de fonctions ;
- la norme « infini » d'un vecteur est la limite de ses normes p lorsque p tend vers l'infini :
-
-
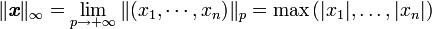
-
- elle induit la distance de déplacement par les faces et par les coins dans un réseau, comme celui du roi sur l'échiquier.
Les relations d'équivalence entre ces normes sont :
L'inégalité triangulaire pour les normes p s'appelle l'inégalité de Minkowski, elle est une conséquence de résultats de convexité parmi lesquels l'inégalité de Hölder.
D'autres exemples apparaissent classiquement :
- La norme sur l'espace des quaternions est la norme euclidienne appliquée à la base (1,i,j,k).
- L'espace des polynômes de degré inférieur ou égal à n peut être muni de normes issues d'espaces de fonctions (voir ci-dessous).
En dimension infinie
- Sur l'espace
![\mathcal C^0([a,b])](https://static.techno-science.net/illustration/Definitions/autres/0/0133ebb09430c2b41a15a9ea543a3233_91a6206e700e175eebe96fde3b5c4a48.png)

-
-
- qui permettent notamment de définir les espaces Lp.
- En particulier, la norme euclidienne associée au produit scalaire ou hermitien canonique est définie par
-
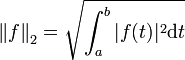
-
- La norme « infini » ou norme sup ou encore norme de la convergence uniforme s'écrit quant à elle
-
- et s'obtient là aussi comme limite des normes p lorsque p tend vers l'infini.
- Toutes ces normes ne sont pas équivalentes deux à deux.
- Par ailleurs elles s'étendent aisément aux espaces de fonctions continues sur un compact de

- Sur l'espace
![\mathcal C^1([a,b])](https://static.techno-science.net/illustration/Definitions/autres/f/f4999edbb0f3735fa50edc185b7653c3_88f5221d0d6a9e43bebefa35d89b0c05.png)
-
-
- afin de considérer l'application dérivée de
![\mathcal C^1([a,b])](https://static.techno-science.net/illustration/Definitions/autres/f/f4999edbb0f3735fa50edc185b7653c3_88f5221d0d6a9e43bebefa35d89b0c05.png)
![\mathcal C^0([a,b])](https://static.techno-science.net/illustration/Definitions/autres/0/0133ebb09430c2b41a15a9ea543a3233_91a6206e700e175eebe96fde3b5c4a48.png)
- Sur l'espace
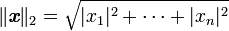
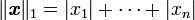
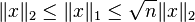
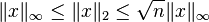
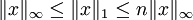
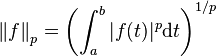
![{\|f\|}_{\infty} = \sup_{t\in [a, b]} |f(t)|](https://static.techno-science.net/illustration/Definitions/autres/8/8a9476448b93458a9e96d731a89b80e0_8deb74637025b0aec0c1c9deef5ce089.png)