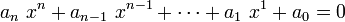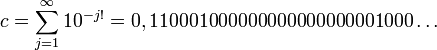Nombre transcendant - Définition

Introduction

En mathématiques, un nombre transcendant sur les rationnels est un nombre réel ou complexe qui n'est racine d'aucune équation polynomiale :

où et les coefficients sont des nombres entiers (donc des rationnels), dont au moins l'un a_n est non nul. Un nombre réel ou complexe est donc transcendant si et seulement s’il n'est pas algébrique.

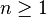
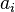
Les nombres transcendants ne sont donc jamais rationnels. Néanmoins, tous les nombres irrationnels ne sont pas transcendants : la racine carrée de 2 est irrationnelle, mais est une solution de l'équation polynomiale .

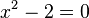
L'ensemble de tous les nombres transcendants est non dénombrable. La démonstration est simple : puisque les polynômes à coefficients entiers sont dénombrables, et puisque chacun de ces polynômes possède un nombre fini de zéros, l'ensemble des nombres algébriques est dénombrable. Mais l'argument de la diagonale de Cantor établit que les nombres réels (et par conséquent les nombres complexes aussi) sont non dénombrables, donc l'ensemble de tous les nombres transcendants doit être non dénombrable. En d'autres termes, il y a beaucoup plus de nombres transcendants que de nombres algébriques. Néanmoins, seules peu de classes de nombres transcendants sont connues et prouver qu'un nombre donné est transcendant peut être extrêmement difficile.

Résultats : considérons l'ensemble A des nombres algébriques réels. Alors :

1. A est un sous-corps de . En particulier, A est stable par addition et multiplication.
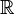
2. A est dénombrable, ce qui montre que A est différent de l'ensemble (les nombres transcendants existent bien).

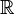
Histoire

Leibniz fut probablement la première personne à croire en l'existence des nombres qui ne satisfont pas les polynômes à coefficients rationnels. Le nom « transcendant » vient de Leibniz dans sa publication de 1682 où il démontra que sin(x) n'est pas une fonction algébrique de x. L'existence des nombres transcendants fut prouvée pour la première fois en 1844 par Joseph Liouville, qui montra des exemples, incluant la constante de Liouville :

dans laquelle le n-ième chiffre après la virgule est 1 si n est une factorielle (l'un des nombres 1, 2, 6, 24, 120, 720, etc.) et 0 sinon ; ce nombre est particulièrement bien approché par les nombres rationnels. Joseph Liouville montra que les nombres ayant cette propriété (que nous nommons maintenant nombres de Liouville) sont tous transcendants ; on trouvera cette démonstration à l'article consacré à ces nombres.

Johann Heinrich Lambert, dans son article prouvant l'irrationalité de conjectura que et étaient des nombres transcendants. Le premier nombre à avoir été démontré transcendant sans avoir été construit spécialement pour cela fut e, par Charles Hermite en 1873. En 1874, Georg Cantor trouva l'argument décrit ci-dessus établissant l'ubiquité des nombres transcendants.

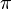
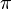
En 1882, Ferdinand von Lindemann publia une démonstration de la transcendance de . Il montra d'abord que e à n'importe quelle puissance algébrique non nulle est transcendant, et puisque est algébrique (voir identité d'Euler), et par conséquent doit être transcendant. Cette approche fut généralisée par Karl Weierstrass avec le théorème de Lindemann-Weierstrass. La transcendance de a permis la démonstration de l'impossibilité de résoudre plusieurs problèmes anciens de construction géométrique avec le compas et la règle, incluant le plus célèbre d'entre eux, la quadrature du cercle.

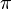
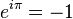
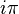
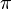
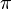
En 1900, David Hilbert a posé une importante question à propos des nombres transcendants, connue sous le nom de septième problème de Hilbert : « Si a est un nombre algébrique non nul et différent de 1 et si b est un nombre algébrique irrationnel, alors le nombre est-il nécessairement transcendant ? » La réponse, affirmative, fut donnée en 1934 par le théorème de Gelfond-Schneider. On peut obtenir facilement des nombres transcendants grâce à lui, par exemple .

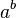
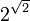
Ce travail fut étendu par Alan Baker dans les années 1960.