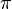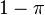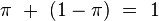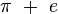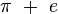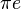Nombre transcendant - Définition
La liste des auteurs de cet article est disponible ici.
Problèmes ouverts
Les nombres dont on ignore s'ils sont transcendants ou non incluent :
-
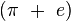
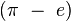
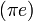

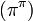
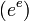
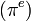
- La constante d'Euler-Mascheroni
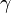
- La constante de Catalan (dont on ignore aussi si elle est irrationnelle)
- La constante d'Apéry
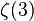
Tous les nombres de Liouville sont transcendants, néanmoins les nombres transcendants ne sont pas tous des nombres de Liouville. Tout nombre de Liouville doit avoir des termes non bornés dans son développement en fraction continue, donc en utilisant un argument de dénombrement, on peut montrer qu'il existe des nombres transcendants qui ne sont pas des nombres de Liouville. En utilisant le développement explicite en fraction continue de e, on peut montrer que e n'est pas un nombre de Liouville. Kurt Mahler montra en 1953 que
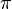
La généralisation du septième problème de Hilbert qui serait de caractériser les transcendants parmi tous les nombres
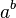

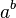

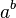

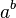
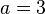
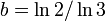
Quelques nombres transcendants connus
- Par le théorème d'Hermite-Lindemann,
- le nombre e (base des logarithmes néperiens), et plus généralement
- les nombres ea pour tout nombre a algébrique non nul ;
- le nombre sin(1), et plus généralement
- les nombres cos(a) et sin(a), pour tout nombre a algébrique non nul.
- Par la contraposée de ce même théorème,
- Le nombre
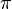
- les nombres log(a) si a est un réel algébrique strictement positif et différent de 1.
- Le nombre
- Par le théorème de Gelfond-Schneider,
- le nombre
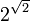
- le nombre réel
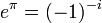
- le nombre réel
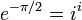
- plus généralement les nombres ab où a est un nombre algébrique différent de 0 et de 1 et où b est algébrique mais non rationnel.
- le nombre
- Par la contraposée de ce même théorème,
- des nombres tels que log(3)/log(2).
- Des nombres tels que xlog(2)+ylog(3)+zlog(5) avec x, y, z algébriques non tous nuls (voir le théorème de Baker).
-
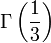
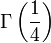
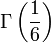
- Le nombre de Champernowne 0,12345678910111213… obtenu en écrivant à la suite les entiers naturels en base dix (théorème de Mahler, 1961)

- où
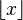
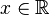
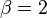
-
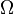
- constante de Prouhet-Thue-Morse
Toute fonction algébrique non constante à une variable donne une valeur transcendante lorsqu'on lui applique une valeur transcendante. Donc, par exemple, en sachant que
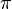
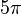
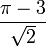
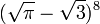
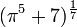
Néanmoins, une fonction algébrique à plusieurs variables peut donner un nombre algébrique lorsqu'elle est appliquée aux nombres transcendants si ces nombres ne sont pas algébriquement indépendants. Par exemple,