Nombre réel - Définition
La liste des auteurs de cet article est disponible ici.
Définitions axiomatiques de R et premières propriétés
On peut caractériser brièvement l'ensemble des nombres réels, que l'on note en général



Approche axiomatique
Une approche axiomatique consiste à caractériser un concept par une série de définitions. Ce point de vue, dont Hilbert est le précurseur dans son formalisme moderne, s'est révélé extrêmement fécond au XXe siècle. Des notions comme la topologie, la théorie de la mesure, ou les probabilités se définissent maintenant par une axiomatique. Une approche axiomatique suppose une compréhension parfaite de la structure en question et permet une démonstration des théorèmes uniquement à partir de ces définitions. C'est la raison pour laquelle de bonnes définitions peuvent en mathématiques s'avérer si puissantes. La définition axiomatique de

La définition axiomatique est essentiellement donnée en introduction :
-

Mais on trouve aussi d'autres définitions axiomatiques qui lui sont équivalentes. Ainsi :
-

-

L'existence et l'unicité d'un tel corps sont démontrées dans l'article Construction des nombres réels, ainsi que l'équivalence entre les deux premières définitions. On y montre de plus que ce corps est nécessairement commutatif, et que le sous-corps des rationnels y est dense.
- L'unicité est à isomorphisme (unique) près, c'est-à-dire que si K est un corps totalement ordonné vérifiant les mêmes hypothèses, alors il existe un (unique) isomorphisme strictement croissant de K dans

-

-

-
 ;
;
-
- L'axiome de la borne supérieure s'exprime de la manière suivante : si un ensemble A de réels est non vide et majoré, autrement dit s'il existe un nombre donné plus grand ou égal à chaque élément de A; alors A admet une borne supérieure, c'est-à-dire un majorant plus petit que tous les autres.
Ce dernier axiome différencie


-

-


Premières propriétés

Musée Alte Meister, Dresden, Allemagne
Cette section est essentiellement technique. Elle traite des propriétés essentielles et élémentaires pour un travail analytique sur

La propriété suivante provient du fait que

- Entre deux réels distincts, il existe toujours un rationnel et un irrationnel.
- Entre deux réels distincts, il existe toujours un rationnel. Soient
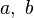
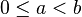
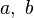

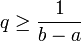
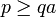
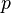
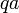
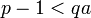
- Entre deux réels distincts, il existe toujours un irrationnel. On utilise que la racine carrée de 2 est irrationnelle. On prend les réels
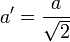
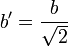

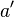
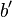
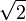
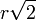


Les autres propriétés sont des conséquences de la propriété de la borne supérieure.
- Tout ensemble non vide et minoré de

- Toute suite croissante et majorée dans

- Toute suite décroissante et minorée dans

- Deux suites adjacentes convergent vers la même limite. On appelle suites adjacentes deux suites, l'une croissante, l'autre décroissante, dont la différence tend vers 0. (Voir l'article Théorème des suites adjacentes.)
Clôture algébrique
Il existe un ensemble de fonctions particulièrement intéressantes, les polynômes. Un polynôme peut parfois être factorisé. C'est-à-dire qu'il s'exprime sous la forme de produit de polynômes non constants de degrés plus petits. L'idéal étant que l'on puisse factoriser tout polynôme en facteurs de degré 1 (c'est-à-dire sous la forme
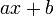
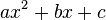
Si

Topologie
La raison d'être des nombres réels est d'offrir un ensemble de nombres avec les bonnes propriétés permettant la construction de l'analyse. Deux approches utilisant deux concepts différents sont possibles.
- On peut utiliser la notion d'espace métrique qui sur

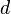
-
-
- Ce concept est le plus intuitif et en général demande des démonstrations un peu plus naturelles. C'est souvent à partir de ce concept que les propriétés analytiques de

- On peut aussi utiliser la théorie de la topologie. Cette théorie est plus générale que celle associée à la distance. Tout espace métrique est associé à un espace topologique. Mais la réciproque n'est pas vraie.
L'élégance favorise la base axiomatique la plus faible. Au XXe siècle un travail de reformulation générale des mathématiques est entrepris par l'association Bourbaki et se traduit par la rédaction d'un ouvrage appelé Éléments de mathématique. Cet ouvrage traite, de manière rigoureuse, d'une vaste partie des mathématiques actuelles. Pour cette raison, les Éléments développent et démontrent les propriétés de l'ensemble des réels à partir de la topologie. C'est le choix que nous suivrons ici.
- Soit
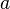
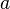
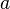
-

-
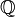

- Les ouverts de

- Les compacts de

- Toutes suites bornée de

-

- Les connexes de

- Théorème des fermés emboîtés. Soit
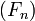
-
 .
.
- En effet, considérons une suite
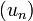
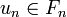
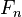
Cardinalité
Combien y a-t-il de nombres réels ? Une infinité, mais laquelle ? Il existe plusieurs cardinaux infinis. Ici cardinal peut se comprendre naïvement comme le nombre d'éléments que contient un ensemble. Dans le cas où les ensembles ne sont pas finis, notre première intuition est trompeuse. Pour comprendre le piège, comparons le cardinal des nombres entiers positifs et des nombres pairs positifs. Notre premier réflexe est de dire que le cardinal des entiers positifs est plus grand car cet ensemble contient, non seulement les nombres pairs mais en plus les nombres impairs, donc deux fois plus de nombres. Puis on peut se dire que l'application qui, à un nombre entier positif, associe le double de ce nombre, montre une correspondance bijective, c'est-à-dire qui associe à chaque nombre de l'ensemble de départ un et un unique élément dans l'ensemble d'arrivée. Notre premier réflexe n'est pas le bon et ne permet pas de construire de théorie des cardinaux. Les deux cardinaux sont en fait égaux. En fait, l'ensemble des entiers positifs et l'ensemble des entiers pairs positifs (ou impairs positifs) correspondent à un même cardinal dit dénombrable. Autrement dit, il y a autant de nombres entiers positifs que de nombres pairs (ou impairs) positifs !
Qu'en est-il du cardinal des nombres rationnels ? Il semble infiniment plus grand que celui des entiers car entre deux entiers il existe une infinité de fractions. Cependant, il est encore possible d'établir une bijection entre l'ensemble des entiers et celui des fractions. La démonstration en est donnée dans l'article ensemble dénombrable.
Posons nous alors la même question pour l'ensemble

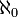

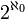
Montrons que le cardinal de l'intervalle
![\left[0,1 \right]\;](https://static.techno-science.net/illustration/Definitions/autres/0/07c34f00a43a07c0c742fce75d5af152_ca3e6ef7e6aa8ccef53c713d5ceaf1e2.png)
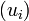
![\left[0,1 \right]\;](https://static.techno-science.net/illustration/Definitions/autres/0/07c34f00a43a07c0c742fce75d5af152_ca3e6ef7e6aa8ccef53c713d5ceaf1e2.png)
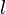
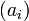
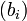
Initialisons nos deux suites par les définitions suivantes :
Il est évident que la propriété (1) est vraie si n est égal à 0. Définissons alors nos suites pour le rang
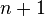
L'intervalle
![\left[a_{n+1},b_{n+1} \right]\;](https://static.techno-science.net/illustration/Definitions/autres/a/ae1b3aaf6bd4f8321f3a915540cec01c_de68019af6f1eafb5e3cdac19eb33606.png)
![\left[a_n,b_n \right]\;](https://static.techno-science.net/illustration/Definitions/autres/a/abe3247157efffe605c3552d8853809f_b4dc8ac6b061a643ad0cdb57a21677f1.png)
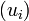
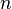
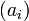
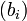
![\left[a_{n+1},b_{n+1} \right]\;](https://static.techno-science.net/illustration/Definitions/autres/a/ae1b3aaf6bd4f8321f3a915540cec01c_de68019af6f1eafb5e3cdac19eb33606.png)
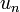
![\left[a_n,b_n \right]\;](https://static.techno-science.net/illustration/Definitions/autres/a/abe3247157efffe605c3552d8853809f_b4dc8ac6b061a643ad0cdb57a21677f1.png)
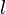
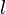
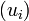
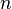
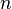


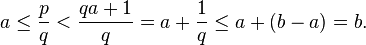
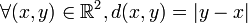
![(1)\quad\forall i<n,\; u_i \;\not\in\; \left[a_n,b_n \right]\;](https://static.techno-science.net/illustration/Definitions/autres/d/d1d56ddfdfe956675ec9912f908e26fb_3b6d742c4d1580c97b1cf8bf8fc22ccb.png)
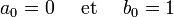
![a_{n+1}=\left\{\begin{matrix} (a_n+2b_n)/3, & \mbox{si }u_n \in \left[a_n,(a_n+b_n)/2 \right] \\ a_n, & \mbox{sinon} \end{matrix}\right.](https://static.techno-science.net/illustration/Definitions/autres/9/9088af9ab9f198ec29e9e560c1990842_87da3d63d928359f68694662a783625a.png)
![b_{n+1}=\left\{\begin{matrix} b_n, & \mbox{si }u_n \in \left[a_n,(a_n+b_n)/2 \right] \\ (2a_n+b_n)/3, & \mbox{sinon} \end{matrix}\right. \;](https://static.techno-science.net/illustration/Definitions/autres/b/b74dda11bde57fee47c44f07589e473a_7525fa5ca068198724fce67ce392f09b.png)

















































