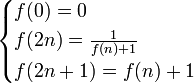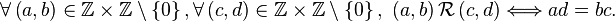Nombre rationnel - Définition

Propriétés

La dénombrabilité des rationnels strictement positifs

L'ensemble , munis des lois d'addition et de multiplication données plus haut, forme un corps, le corps des fractions des entiers .

Les rationnels sont le plus petit corps de caractéristique nulle. Tout autre corps de caractéristique nulle contient une copie de .

La clôture algébrique de , c'est-à-dire le corps des racines des polynômes à coefficients rationnels est l'ensemble des nombres algébriques.

L'ensemble des rationnels est dénombrable. Or par l'argument de la diagonale de Cantor, nous savons que le corps des nombres réels ne l'est pas. On dit alors que les nombres réels sont presque tous irrationnels, au sens de la mesure de Lebesgue. On dit que est un ensemble négligeable.

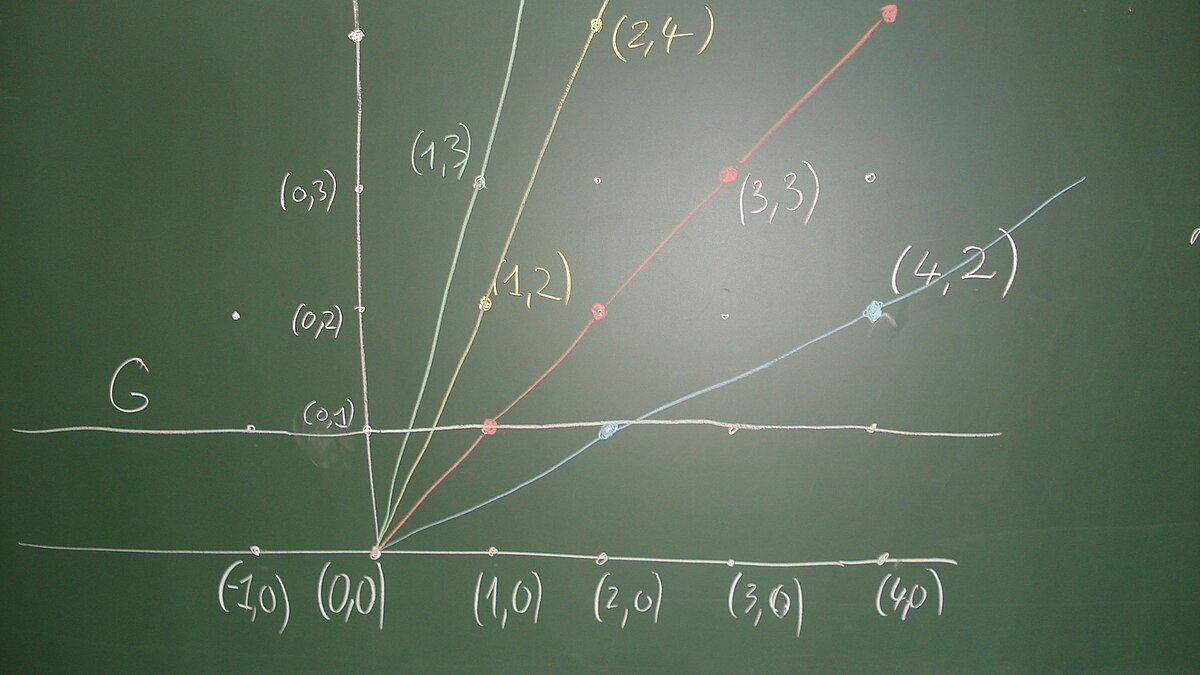
La fonction f suivante, bijective de dans , donne tous les nombres rationnels positifs ou nuls, avec le numérateur et le dénominateur toujours premiers entre eux par construction. Elle est inspirée des suites de Farey :

Elle s'inverse par la fonction g suivante :

Construction formelle

On peut voir un nombre rationnel comme la classe d'équivalence d'une paire ordonnée d'entiers, par la relation d'équivalence suivante:

On note alors , c'est-à-dire que l'ensemble des nombres rationnels est le quotient de par la relation d'équivalence.

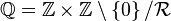
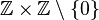
On peut ensuite injecter les entiers dans les rationnels, et définir des lois de composition interne pour se donner une structure de corps.

Cette construction est valable à partir de n'importe quel anneau intègre, on parle alors de corps des fractions.

Nombre p-adique

On peut munir d'une autre métrique.

Soit p un nombre premier et notons, pour tout entier non nul a:

| a | _p = p ^{− n},

où pⁿ est la plus grande puissance de p divisant a.

Arbitrairement, on pose | 0 | _p = 0. Puis pour chaque nombre rationnel a / b, on pose : .

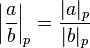
Alors définit un espace métrique.

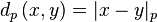
L'espace métrique n'est pas complet, et sa complétion est le corps des nombres p-adique . Le théorème d'Ostrowski montre que toute valeur absolue non triviale sur est équivalente, soit à la valeur absolue usuelle, soit à une valeur absolue p-adique.

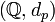
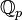
Topologie

Muni de la topologie de l'ordre usuelle, Q est un corps topologique. Cela signifie que les opérations arithmétiques sont continues. L'addition est de plus compatible avec l'ordre (on parle de groupe ordonné).

Limitations

Par contre, Q ne possède pas la propriété de la borne supérieure : l'ensemble des nombres rationnels x tels que x² < 2 est majoré mais ne possède pas de plus petit majorant.

D'autre part, Q n'est pas un espace complet : il existe des suites de Cauchy de nombres rationnels qui ne convergent pas vers un nombre rationnel, comme par exemple la suite (x_n) définie par récurrence suivant la méthode de Héron :

• x₀ = 1
• pour tout n entier naturel non nul : x_n+1 = ^x_n ⁄₂ + ¹⁄_xn.

Ces deux limitations montrent notamment que des nombres essentiels en mathématiques, comme √2 ou π, ne sont pas rationnels. Cela conduit à compléter Q en construisant un ensemble plus grand, qui possède la propriété de la borne supérieure et dans lequel toute suite de Cauchy converge : l'ensemble des nombres réels.