Nombre premier - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs (qui sont alors 1 et lui-même). Cette définition exclut 1, qui n'a qu'un seul diviseur entier positif. Par opposition, un nombre non nul produit de deux nombres entiers différents de 1 est dit composé. Par exemple 6 = 2 × 3 est composé, tout comme 21 = 3 × 7 ou 7 × 3, mais 11 est premier car 1 et 11 sont les seuls diviseurs de 11. Les nombres 0 et 1 ne sont ni premiers ni composés. Les nombres premiers inférieurs à 100 sont :
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 et 97.
De telles listes peuvent être obtenues grâce à diverses méthodes de calcul. On sait depuis l'Antiquité qu'il existe une infinité de nombres premiers. Découvert en 2008, le plus grand nombre premier connu est le nombre premier de Mersenne « 243 112 609-1 », qui comporte près de 13 millions de chiffres en écriture décimale. La notion de nombre premier est une notion de base en arithmétique élémentaire : le théorème fondamental de l'arithmétique assure qu'un nombre composé est factorisable en un produit de nombres premiers, et cette factorisation est unique à l'ordre des facteurs près. Elle admet des généralisations importantes dans des branches des mathématiques plus avancées, comme la théorie algébrique des nombres, qui prennent ainsi à leur tour l'appellation d'arithmétique. Par ailleurs, de nombreuses applications industrielles de l'arithmétique reposent sur la connaissance algorithmique des nombres premiers, et parfois plus précisément sur la difficulté des problèmes algorithmiques qui leur sont liés ; par exemple certains systèmes cryptographiques et des méthodes de transmission de l'information. Les nombres premiers sont aussi utilisés pour construire des tables de hachage et pour constituer des générateurs de nombres pseudo-aléatoires.
Éléments historiques
Les entailles retrouvées sur l’os d'Ishango daté à plus de 20 000 ans avant notre ère, mis au jour par l'archéologue Jean de Heinzelin de Braucourt et antérieur à l'apparition de l'écriture (antérieur à 3 200 ans avant J.-C.), semblent isoler quatre nombres premiers 11, 13, 17 et 19. Certains archéologues l'interprètent comme la preuve de la connaissance des nombres premiers. Toutefois, il existe trop peu de découvertes permettant de cerner les connaissances réelles de cette période ancienne.
Des tablettes d'argile séchées attribuées aux civilisations qui se sont succédé en Mésopotamie durant le IIemillénaire av. J.-C. montrent la résolution de problèmes arithmétiques et attestent des premières connaissances de l'époque. Les calculs nécessitaient de connaître des tables d'inverses d'entiers (les réciproques) dont certaines ont été retrouvées. Dans le système sexagésimal utilisé par la civilisation babylonienne pour écrire les entiers, les réciproques des diviseurs des puissances de 60 (nombres réguliers) se calculent facilement : par exemple, diviser par 24, c'est multiplier par
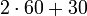
Dans les mathématiques égyptiennes, le calcul fractionnaire demandait des connaissances sur les opérations, les divisions d’entiers et les factorisations. Les Égyptiens ne notaient que les inverses d’entiers (1/2, 1/3, 1/4, 1/5, ...) ; l’écriture des fractions se faisait en additionnant des inverses d'entiers, si possible sans répétition (1/2 + 1/6 au lieu de 1/3 + 1/3). Disposer d’une liste des premiers nombres premiers devait être nécessaire.
La première trace incontestable de la présentation des nombres premiers remonte à l'Antiquité (vers -300 av. J.-C.), et se trouve dans les Éléments d’Euclide (tomes VII à IX). Euclide donne la définition des nombres premiers, la preuve de leur infinité, la définition du plus grand commun diviseur (pgcd) et du plus petit commun multiple (ppcm), et les algorithmes pour les déterminer, aujourd’hui appelés algorithmes d’Euclide. Les connaissances présentées lui sont toutefois bien antérieures.


















































