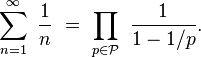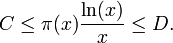Nombre premier - Définition
La liste des auteurs de cet article est disponible ici.
Applications
Les nombres premiers, et la théorie des nombres en particulier, ont longtemps été vus comme un sujet purement mathématique, avec peu ou pas d'applications extérieures. Cela changea d'un seul coup dans les années 1970, quand des nouveaux systèmes de cryptographie basés sur les propriétés des nombres premiers furent découverts.
Cryptographie à clé publique
Jusque dans les années 1970, les systèmes de chiffrement connus étaient basés sur le principe de la cryptographie symétrique, où une même clé (secrète) est utilisée pour chiffrer et déchiffrer un message. En 1978, Ronald Rivest, Adi Shamir et Leonard Adleman décrivent le premier système public de cryptographie asymétrique (nommé d'après eux RSA), basé sur les propriétés des nombres premiers et de la factorisation. Dans un tel système, deux clés sont utilisées : l'une sert à chiffrer, l'autre à déchiffrer. La clé permettant de chiffrer est accompagnée d'un grand nombre entier, le produit de deux grands nombres premiers gardés secrets (de l'ordre de 200 chiffres). Pour calculer la clé de déchiffrement, la seule méthode connue nécessite de connaître les deux facteurs premiers. La sécurité du système est basée sur le fait qu'il est facile de trouver deux grands nombres premiers (en utilisant des tests de primalité) et de les multiplier entre eux, mais qu'il serait difficile pour un attaquant de retrouver ces deux nombres. Ce système permet également de créer des signatures numériques, et a révolutionné le monde de la cryptographie.
Répartition des nombres premiers
Infinité des nombres premiers
Euclide a démontré dans ses Éléments (proposition 20 du Livre IX) que les nombres premiers sont en plus grande quantité que toute quantité proposée de nombres premiers. Autrement dit, il existe une infinité de nombres premiers. La démonstration d'Euclide repose sur la constatation qu'une famille finie p1,...,pn de nombres premiers étant donnée, tout nombre premier divisant le produit des éléments de cette famille augmenté de 1 est en dehors de cette famille (et un tel diviseur existe, ce qui est aussi prouvé par Euclide).
D'autres démonstrations de l'infinité des nombres premiers ont été données. La preuve d'Euler utilise l'identité :
Dans la formule précédente, le terme de gauche est la somme de la série harmonique, qui est divergente. Par conséquent, le produit de droite doit contenir une infinité de facteurs.
Furstenberg fournit une preuve utilisant une argumentation topologique.
Les avancées du XIXe siècle
Le résultat sur l'infinité des nombres premiers amène des questions plus précises concernant la fonction qui à un nombre réel x associe π(x), le nombre de nombres premiers inférieurs à x, et qui tend donc vers l'infini. Une conjecture importante au XIXe siècle, formulée par Adrien-Marie Legendre et Carl Friedrich Gauss, était que cette fonction de compte des nombres premiers est équivalente à la fonction
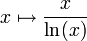
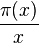
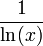
L'inégalité de Tchebychev permettait notamment de démontrer le postulat de Bertrand selon lequel dans tout intervalle d'entiers naturels entre un entier et son double existe au moins un nombre premier. Plus généralement, les résultats sur la fonction de compte des nombres premiers permettent d'obtenir des résultats sur le ne nombre premier ; par exemple les résultats d'Ishikawa de 1934 sont des conséquences directes des théorèmes de Tchebychev : pn + pn + 1 > pn + 2 et pnpm > pn + m, où pn désigne le ne nombre premier (et donc p1=2) ; ou encore, d'après un résultat de Felgner de 1990 : 0,91 n ln(n) < pn < 1,7 n ln(n).
La démonstration analytique d'Euler sur l'infinité des nombres premiers peut être vue comme un premier pas vers la résolution de problèmes plus avancés. Elle consiste essentiellement à étudier le comportement de la fonction zêta de Riemann en 1 au moyen de ce qu'il est convenu d'appeler un produit eulérien, et d'en déduire la divergence de la série des inverses des nombres premiers. En reprenant cette étude, au moyen d'un outil appelé caractère de Dirichlet, et en utilisant à la place de la fonction zêta de Riemann des fonctions analogues appelées fonction L de Dirichlet, Dirichlet a été capable d'adapter la démonstration aux nombres premiers dans des progressions arithmétiques : si a et b sont premiers entre eux, alors il existe une infinité de nombres premiers de la forme aq+b. Plus précisément, les nombres premiers sont équirépartis entre les différentes progressions arithmétiques de raison a (c'est-à-dire avec a fixé, et b variant parmi les divers restes inversibles dans la division euclidienne par a).
La conjecture de Legendre et Gauss a été démontrée indépendamment par Jacques Hadamard et Charles-Jean de La Vallée Poussin en 1896, et porte le nom de théorème des nombres premiers. Ces démonstrations nécessitent des outils puissants d'analyse complexe pour démontrer un énoncé d'arithmétique et d'analyse réelle. Une stratégie pour ces démonstrations est l'étude de la fonction zêta de Riemann sur un domaine plus grand qu'un simple voisinage de 1 : il est nécessaire de la contrôler (c'est-à-dire majorer son module) au voisinage de la droite verticale des nombres de partie réelle 1 dans le plan complexe. En particulier, l'étude de la fonction zêta de Riemann devient un thème central en théorie analytique des nombres, en particulier l'hypothèse de Riemann sur la localisation de ses zéros, encore non démontrée, qui aurait des conséquences fortes sur l'étude de la fonction de compte des nombres premiers. Ultérieurement, des démonstrations ont été proposées sans recours à l'analyse complexe (par Erdös et Selberg au milieu du XXe siècle). Toutefois, la puissance des outils d'analyse complexe a conduit au développement d'une branche entière des mathématiques : la théorie analytique des nombres.
Théorème de Green-Tao
Un théorème démontré en 2004 par Ben Joseph Green et Terence Tao généralise notamment le théorème de Dirichlet en assurant que pour tout entier k, il existe une infinité de suites de k nombres premiers en progression arithmétique, c'est-à-dire de la forme :
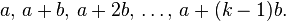
Le théorème de Green-Tao est en fait bien plus fort que cet énoncé seul : par exemple, ils sont en mesure d'affirmer qu'une telle progression arithmétique existe, avec des entiers tous plus petits que :
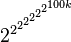
Ils assurent aussi que pour tout entier k et tout réel δ strictement positif, pour tout x suffisamment grand, si P est un ensemble de nombre premiers inférieurs à x contenant au moins δπ(x) éléments, alors P contient au moins une progression arithmétique de nombres premiers comptant k termes.
Conjecture de Bateman-Horn
De nombreux résultats et conjectures sur la répartition des nombres premiers sont contenus dans la conjecture générale suivante. Soit f1,...,fk des polynômes de degré 1, irréductibles et vérifiant la propriété que pour tout nombre premier p il y ait au moins un entier n parmi 0, ..., p-1 tel que p ne divise pas le produit des fi(n). On note ω(p) le complémentaire à p du nombre de tels entiers. Un tel ensemble de polynômes est dit admissible ; on cherche à connaître la proportion d'entiers en lesquels les polynômes prennent simultanément des valeurs premières, et se limiter à des ensembles de polynômes admissibles permet d'éviter des cas triviaux comme f1(t)=t, et f2(t)=t+1. Il est alors conjecturé que le nombre d'entiers n plus petits qu'un réel x tels que les valeurs f1(n),...,fk(n) sont simultanément premières, est, pour x assez grand, de l'ordre de :
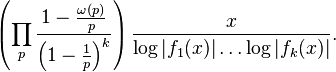
Le théorème des nombres premiers correspond au cas k=1 et ft=t, le théorème de Dirichlet à k=1 et ft=at+b, et pour k=2, f1(t)=t et f2(t)=t+2, on obtient une version quantitative (et donc plus générale) de la conjecture des nombres premiers jumeaux.