Nombre ordinal - Définition

Utilisation des ordinaux

En dehors d'utilisations spécifiques à la théorie des ensembles, les ordinaux se rencontrent dans les domaines suivants :

En arithmétique

Le théorème de Goodstein est un théorème d'arithmétique dont la démonstration repose sur la théorie des ordinaux. Ce théorème pose la question de savoir si une certaine suite à valeurs entières finit par prendre la valeur 0. On associe à cette suite d'entiers une suite d'ordinaux strictement décroissante. Compte tenu du bon ordre des ordinaux, une telle suite est effectivement finie. La suite possède une définition relativement simple, pourtant on peut démontrer que le théorème de Goodstein n'est pas démontrable en utilisant uniquement les propriétés de l'arithmétique usuelle et donc que l'utilisation des ordinaux infinis permet de démontrer des résultats arithmétiques indécidables dans l'arithmétique.

En analyse

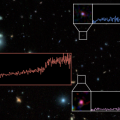
Les ordinaux ont été définis par Cantor à la suite de ses études sur la convergence des séries trigonométriques. Si une telle série est nulle sur , alors tous les coefficients a_n et b_n sont nuls. Cantor va chercher à affaiblir les hypothèses en réduisant le domaine sur lequel la série s'annule. Il montre que le résultat reste vrai si la série est nulle sauf en un nombre fini de points. Puis il introduit la notion suivante. Si P est une partie d'un segment [a,b], il définit l'ensemble dérivé de P, noté P¹ comme l'ensemble des points d'accumulation de P ou, de manière équivalente, comme l'ensemble P duquel ont été retiré tous les points isolés. Pour tout entier n, il définit P^{n + 1} comme étant le dérivé de l'ensemble Pⁿ. Il montre que, si la série trigonométrique est nulle sur [0,2π] en dehors d'un ensemble P pour lequel l'un des Pⁿ est vide, alors les coefficients sont nuls.

Cherchant à prolonger ce résultat si les Pⁿ sont tous non vides. Il définit alors , puis P^{ω + 1} comme étant le dérivé de P^ω. D'une manière générale, on définit, pour tout ordinal α l'ensemble P^{α + 1} comme étant l'ensemble dérivé de P^α, et si α est un ordinal limite, P^α comme étant .

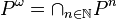
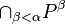
René Baire reprendra cette démarche pour la convergence simple des suites de fonctions continues vers une fonction discontinue. Il définit une partie réductible P comme une partie pour laquelle il existe un ordinal α tel que P^α soit vide. Baire montre ensuite que si f est une fonction telle que l'ensemble des points où elle est discontinue est un ensemble réductible, alors f est limite simple d'une suite de fonctions continues.

Dans le cas contraire, la suite des P^α se stabilise à l'ensemble P^Ω, où Ω désigne le premier ordinal non dénombrable. On montre que P^Ω est un ensemble parfait.

En topologie

Soit Γ un ordinal. Notons [0,Γ] l'ensemble des ordinaux inférieurs ou égaux à Γ. Cet ensemble peut être muni d'une structure topologique, en prenant comme prébase d'ouverts les parties et pour tout ordinal α et β inférieurs ou égaux à Γ. Ces topologies sont sources de nombreux exemples et contre-exemples.

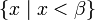
Ainsi, si on prend Γ = ω, alors [0,ω[ est l'ensemble muni de sa topologie discrète usuelle. [0,ω] est un compactifié de .

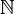
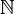
Si on prend Γ = Ω premier ordinal non dénombrable, alors aucune suite strictement inférieure à Ω ne peut converger vers Ω, bien que Ω appartienne à l'adhérence de [0,Ω[. En particulier, Ω n'admet pas de base dénombrable de voisinages et c'est le seul point de [0,Ω] qui soit dans ce cas.

Dans tout espace [0,Γ], les points de la forme α + 1 sont isolés. [0,Γ] est un espace compact. [0,Γ] et [0,Γ[ sont des espaces topologiques normaux. est normal mais pas complètement normal. est complètement régulier mais n'est pas normal. [0,Ω] est complètement normal, mais pas parfaitement normal. est faiblement normal mais pas normal.

Une construction similaire donne naissance à la longue droite, un espace topologique analogue à la droite réelle, mais « beaucoup plus long ».