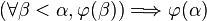Nombre ordinal - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
On montre que :
- Si deux ordinaux α et β sont donnés, alors ou bien
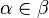
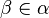
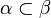
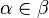
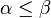
- Tous les éléments d'un ordinal sont des ordinaux.
- Si
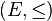
- L'intersection de deux ordinaux est un ordinal, égal au plus petit des deux ordinaux.
- La réunion de deux ordinaux est un ordinal, égal au plus grand des deux ordinaux.
- Si α est un ordinal,
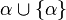
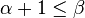
- Si A est un ensemble dont les éléments sont des ordinaux, alors
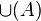
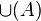
- Si α est un ordinal non vide, alors :
-
- ou bien α possède un élément maximal β. Alors
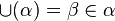
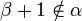
- ou bien α ne possède pas d'élément maximal. Alors
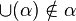
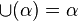
- ou bien α possède un élément maximal β. Alors
- On dit que l'ordinal α est fini si α n'est pas un ordinal limite et ne contient aucun ordinal limite ; autrement dit α est infini s'il existe un ordinal limite
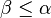
- Récurrence transfinie. Cette récurrence généralise le principe de récurrence qu'on applique sur les entiers à tous les ordinaux. Si

-
-
- alors
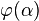
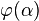
- On utilise souvent une variante de ce principe pour définir une fonction
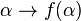
- Cas de base : f(0) = X0 où X0 est un ensemble donné ;
- Cas successeur : f(α + 1) = g(α,f(α)) où g est une fonction donnée ;
- Cas limite :
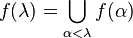
- Les deux premiers cas sont les deux usuels de la récurrence sur les entiers, le troisième est nécessaire pour étendre le schéma à tous les ordinaux.
Définition
On définit un nombre ordinal de l'une des deux manières suivantes :
- La première définition est basée sur les classes d'équivalence d'ensembles ordonnés. Un ordinal est un ensemble bien ordonné, considéré à un isomorphisme d'ordre près (dans la catégorie des bons ordres où les morphismes sont les applications croissantes et les isomorphismes les bijections croissantes). Ainsi, si on change les noms des éléments d'un bon ordre, tant qu'on ne change pas la manière dont les éléments se comparent entre eux, on parle toujours du même ordinal.
- La seconde définition est due à John von Neumann, et traduit le fait qu'un ordinal est défini par l'ensemble des ordinaux qui le précèdent. Un ordinal α est un ensemble vérifiant les deux propriétés suivantes :
-
- (i) La relation d'appartenance ∈ sur cet ensemble est un bon ordre strict (c'est-à-dire un ordre strict dont l'ordre large associé est un bon ordre).
- (ii) Cet ensemble est transitif, ce qui signifie que :
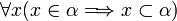
C'est cette dernière définition que nous adopterons dans la suite de l'article. Usuellement, les ordinaux sont désignés par des lettres grecques, les ensembles en général par des lettres latines.
En appliquant la définition précédente, les entiers naturels peuvent être construits de la façon suivante :
- 0 = {} (ensemble vide)
- n+1 = n U {n}
Un entier positif est ainsi identifié à l'ensemble de ses prédécesseurs sur N. Exemples :
- 1 = {0} = { {} }
- 2 = {0,1} = { {}, { {} } }
- 3 = {0,1,2} = {{}, { {} }, { {}, { {} } }}
- 4 = {0,1,2,3} = { {} , { {} }, { {}, { {} } } , {{}, { {} }, { {}, { {} } }} } etc.
De cette manière, tout entier naturel est un ensemble bien ordonné par la relation d'appartenance
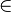
L'existence des ordinaux infinis est assuré par l'axiome de l'infini. Le premier nombre ordinal transfini (i.e. infini) est noté ω. Il correspond à l'ensemble des nombres entiers naturels
L'ordinal qui suit est
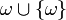
Pour définir une notation adaptée aux ordinaux suivants, nous aurons besoin de définir des opérations arithmétiques sur les ordinaux.
Les ordinaux sont totalement ordonnés au sens large par l'inclusion ou au sens strict par l'appartenance, mais ne forment pas un ensemble au sens des axiomes ZFC (la théorie des ensembles habituelle), mais une classe propre. Ceci peut-être mis en évidence grâce au paradoxe de Burali-Forti : l'ensemble des ordinaux serait par définition un ordinal ... mais qui serait strictement plus grand (aussi par définition) que tous les ordinaux. Et donc que lui-même, ce qui est contradictoire.