Nombre de Reynolds - Définition

Interprétation du nombre de Reynolds

Le nombre de Reynolds peut s'écrire de la manière suivante :

,

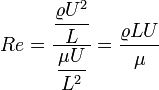
Il s'interprète alors comme le rapport entre forces d'inertie et forces visqueuses. On distingue trois principaux régimes.

• Aux faibles valeurs du Reynolds (inférieures à 2000), les forces de viscosité sont prépondérantes, l'accélération convective étant négligée ; c'est par exemple le cas en microfluidique. On parle d'écoulement de Stokes. L'écoulement est laminaire (des éléments de fluide voisins demeurent voisins). De plus, comme l'inertie est négligeable, l'écoulement du fluide est réversible. Cela donne lieu à des comportements surprenants : si les forces extérieures sont soudainement stoppées, le fluide s'arrête immédiatement. Qui plus est, si les forces extérieures sont inversées, le fluide repart en sens inverse : dans une célèbre expérience de G.I.Taylor, une goutte d'encre, initialement mélangée dans un fluide visqueux, se reconstitue lorsque l'on inverse le mouvement.
• Aux valeurs intermédiaires du Reynolds (entre 2000 et 3000 environ), les forces d'inertie sont prépondérantes, mais l'écoulement reste laminaire. Cependant, il n'est plus réversible: si l'on stoppe les forces extérieures, le fluide continue partiellement sur sa lancée.
• Aux fortes valeurs du Reynolds (au-delà d'environ 3000, voire plus haut), les forces d'inertie sont si importantes que l'écoulement devient turbulent. Entre les régimes laminaire et turbulent, on parle de régime transitoire.

La similitude des fluides

Deux écoulements à géométrie équivalente pour lesquels les nombres de Reynolds sont égaux sont dits semblables. Pour qu'une expérience de modèle réduit d'un écoulement donne bien un écoulement semblable (c'est-à-dire identique à changements d'échelles de temps, de distance et de masse près) à l'écoulement en grandeur nature, il faut que :

et

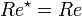
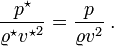
Les valeurs marquées d'une astérisque « * » font référence à l'écoulement dans le modèle réduit et les autres valeurs à l'écoulement en grandeur nature. Ceci est utile pour les expériences sur les modèles réduits en veine liquide ou en tunnel aérodynamique où on récupère les données pour les écoulements en grandeur réelle. Pour les fluides compressibles, les nombres de Mach doivent aussi être égaux pour les deux fluides afin qu'ils puissent être considérés comme équivalents. De manière générale, il faut que les nombres sans dimension caractéristiques de l'écoulement soient identiques dans les deux écoulements.