Nombre d'or - Définition
La liste des auteurs de cet article est disponible ici.
Arithmétique
Un autre chemin que celui de la géométrie permet de mieux comprendre les propriétés du nombre d'or, l'arithmétique. Elle met en évidence ses propriétés algébriques ainsi que les profondes relations entre des sujets apparemment aussi différents que la suite de Fibonacci ou sa relation avec de difficiles équations diophantiennes. Une équation diophantienne est une équation dont les coefficients sont entiers et dont les solutions recherchées sont entières. Pour citer un exemple célèbre, celui-ci correspond à un cas particulier du dernier théorème de Fermat :
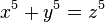
Il fut résolu par Dirichlet en 1825, ce qui lui valut une célébrité immédiate. Carl Friedrich Gauss , un mathématicien du XIXe siècle disait des problèmes de cette nature : « Leurs charmes particuliers vient de la simplicité des énoncés jointe à la difficulté des preuves. »
À l'aide d'outils un peu ésotériques, comme la fraction continue ou l'entier algébrique, une arithmétique du nombre d'or, plus communément appelé arithmétique de Dirichlet, se dessine. Les repères sont modifiés par rapport à ceux des entiers naturels. Le nombre d'or est considéré comme un entier à cause de son analogie avec la situation plus classique. On ajoute en général le terme algébrique ou quadratique pour marquer la différence. Dans cet univers, 19 n'est pas un nombre premier, au sens de Dirichlet.
Fraction continue
La fraction continue est une manière d'approcher un nombre réel, dans le cas du nombre d'or, elle est simple. On peut l'approcher par les valeurs 1 ou 1 + 1/1. La fraction suivante est plus précise :
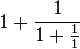
Le prolongement à l'infini de cette méthode donne exactement le nombre d'or :
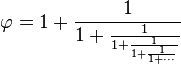
Le fait que la fraction ne s'arrête jamais montre que le nombre d'or n'est pas un nombre rationnel. Une démonstration est proposée dans l'article détaillé. On reconnaît, sous la première barre de fraction l'expression du nombre d'or. On en déduit plusieurs expressions algébriques de φ :
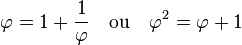
La dernière formule donne une nouvelle expression du nombre d'or :
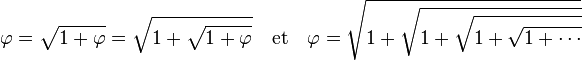
Cette propriété possède des conséquences remarquables si φ est utilisé comme base d'un système de nombre (voir base d'or).
La fraction continue approximant le nombre d'or possède systématiquement la plus petite valeur possible pour chacun de ses coefficients, à savoir 1. En conséquence, il est le nombre irrationnel qui s'approxime le plus mal par des rationnels. On dit de lui qu'il est le plus irrationnel des nombres réels (cf. Théorème d'Hurwitz).
Une démonstration plus classique et rigoureuse est proposée dans l'article détaillé.
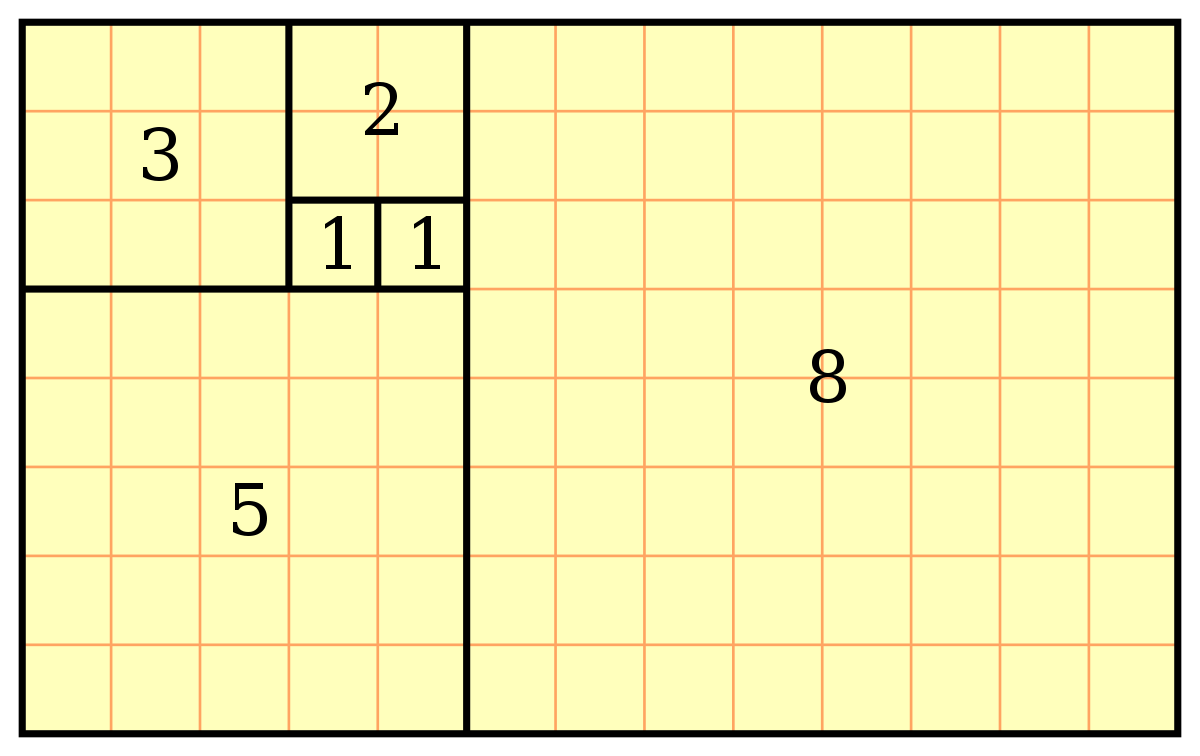
Une manière d'illustrer la fraction continue est la suivante. Dans un premier temps, on dessine un rectangle formé de deux carrés côte à côte et de côté 1. Ce sont les deux carrés numérotés 1 sur la figure de droite. Le rapport entre la longueur et la largeur de la figure est égal à 2, la meilleure approximation en nombre entier du nombre d'or. On ajoute un carré de côté égal à la longueur de la figure précédente. Un tel carré est de côté 2 qu'il est judicieux d'écrire ici 1+1. On obtient un rectangle, composé de trois carrés (les deux numérotés 1 et celui numéroté 2) dont le rapport de la longueur sur la largeur est égal 3/2 qui s'écrit 1 + 1/2 ou encore 1 + 1/(1+1). On réitère avec un carré de côté égal à la longueur du rectangle précédent, soit celui numéroté 3 sur la figure, on trouve :
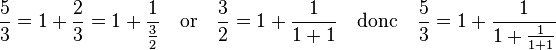
L'approximation commence à être précise, elle vaut 1,66..., celle du nombre d'or est 1,62... On recommence le processus avec un carré de côté la longueur du précédent, on obtient comme rapport 8/5, qui s'écrit 1 + 3/5 et avec le calcul précédent :
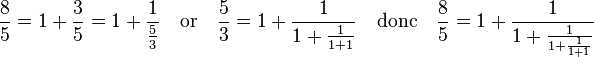
La dernière itération de la figure donne un rectangle dont le rapport de la longueur sur la largeur vaut 13/8 approximation précise à plus de un centième. Si le processus est réitéré à l'infini, on obtient une expression du nombre d'or en fraction continue :
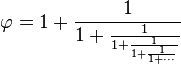
Ce résultat possède une conséquence géométrique déjà citée. Si le processus de génération de rectangle est itéré un nombre suffisant de fois. Le retrait d'un carré de dimension maximale laisse une surface rectangulaire de même proportion que le rectangle initial, aux erreurs de mesure près. On obtient un rectangle d'or.
Suite de Fibonacci
Le calcul des couples de numérateurs et dénominateurs obtenus par la fraction continue donne les valeurs suivantes (1,1), (2,1), (3,2), (5,3) ... le dénominateur correspond au numérateur de la fraction précédente. Il est aussi égal au nième terme de la suite de Fibonacci (un). Elle est définie par récurrence :
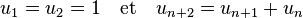
Les deux premiers termes sont égaux à 1 et les autres à la somme des deux précédents. Pour obtenir une bonne approximation du nombre d'or, il suffit de choisir une valeur de n suffisamment élevée et considérer la fraction un+1/un. En terme mathématiques, cela s'exprime sous la forme suivante :
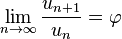
La vitesse de convergence est grande, la différence entre un+1/un et φ est, en valeur absolue, inférieure au carré de un.
Si la suite de Fibonacci permet de déterminer une approximation du nombre d'or, la réciproque est vraie. Plus exactement, on dispose de la formule suivante :
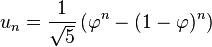
La valeur |1-φ|n ne fait que diminuer lorsque n s'accroît, elle est toujours suffisamment petite pour pouvoir être négligée, il suffit de prendre l'entier le plus proche de l'expression précédente en négligeant le terme en (1 - φ)n, on obtient :
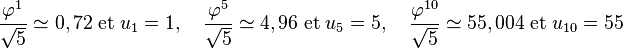
Cette propriété est vérifiée pour toute suite définie par la relation de récurrence un+2 = un+1 + un, indépendamment des valeurs prises par u1 et u2.
-
- La suite un+1/un tend vers le nombre d'or :
Ce résultat peut se voir comme une conséquence de la construction graphique du paragraphe précédent. Le dénominateur est le numérateur de la fraction continue. Les deux premiers dénominateurs sont égaux à 1 et le numérateur est bien la somme des deux numérateurs précédents.
-
- La suite (1/√5.φn) s'approche infiniment de celle de Fibonacci :
Pour utiliser la dimension géométrique du nombre d'or, considérons-les dans la suite de vecteurs d'un plan euclidien et coordonnées (un, un-1).
La fonction f qui à (un, un-1) associe (un+1, un) est une application linéaire. Son comportement devient clair s'il est analysé sur deux axes, de vecteurs directeurs u = (1, φ) et v = (1, -φ). Sur l'axe u, la fonction f est une homothétie de rapport φ, chaque vecteur sur la droite dirigée par u est multiplié par φ. Si la fonction f est appliquée n fois, alors le rapport de l'accroissement est de φn. Sur l'axe v, la fonction est encore une homothétie, mais de rapport 1 - φ. Comme 1 - φ est un nombre négatif strictement plus petit que 1 en valeur absolue, à chaque itération, un vecteur sur la droite dirigé par v change de direction et se trouve comprimé d'un rapport 1 - φ.
Le point initial p0 = (u2, u1) peut être décomposé sur les deux vecteurs u et v, on trouve p0 = 1/2 (u + v). Calculer p1 = (u3, u2) puis p2 puis pn devient simple, il suffit d'appliquer la fonction f une puis deux puis n fois :
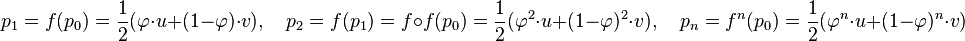
On obtient la formule :
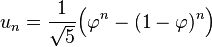
Le terme en (1 - φ) est positif et strictement plus petit que 1. Les puissances (1 - φ)n s'approchent en conséquence de plus en plus de 0.
Équation diophantienne
La fraction continue offre des rationnels b/a offrant presque des solutions à l'équation qui s'écrit sous les formes suivantes :
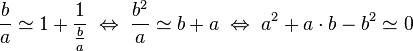
L'égalité stricte à zéro est impossible, elle n'autorise que les solutions triviales. En effet, aucun nombre rationnel ne vérifie la proportion d'or, ce qui justifie l'équation diophantienne suivante :
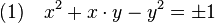
L'école mathématique indienne s'intéresse aux équations de cette nature. Brahmagupta développe une méthode, dite chakravala qui permet l'étude de telles équations. Il utilise une identité, qui dans le cas présent prend la forme suivante :
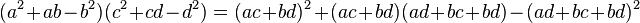
Cette identité est liée à l'équation (1) précédente et donc au nombre d'or. Si (a, b) et (c, d) forment deux couples, solutions de l'équation (1), la partie de gauche de l'identité est égale à plus ou moins un. La partie de droite de l'identité décrit donc une solution (e, f) si e = ac + bd et f = ad + bc + bd. La découverte d'une multiplication particulière *, permet de construire autant de solutions que désiré, à partir d'une unique si elle n'est pas triviale :
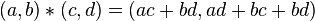
En combinant une solution (a, b) avec elle-même on en obtient une nouvelle (a2 + b2, 2a.b + b2). Le couple (1, 1) est solution de l'équation (1), donc le couple (2, 3) l'est aussi. Elle est d'ailleurs déjà obtenue avec la méthode précédente. Avec la solution (2, 3) on obtient (13, 21) et avec la solution (13, 21) on obtient (610, 987). On vérifie que le couple (610, 987) est bien une solution de l'équation :
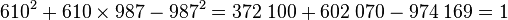
On en déduit que la fraction 987/610 est une excellente approximation du nombre d'or. En effet, 987/610 = 1,6180327... une précision proche du millionième.
Entier de Dirichlet
Dans cette vision du nombre d'or, il existe une multiplication naturelle. L'adjonction de l'addition usuelle des couples d'entiers relatifs, définit par l'égalité suivante, confère à l'ensemble des couples (a, b) une structure équipée d'une addition et d'une multiplication appelé, en terme contemporain, un anneau.
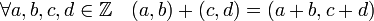
Si cet anneau est construit à partir d'une équation diophantienne connexe au nombre d'or, sa relation avec φ peut être vue plus directement. Il se conçoit simplement en considèrant les nombres réels de la forme a + φ.b, où a et b désignent deux nombres entiers. L'identité de Brahmagupta, définissant la multiplication se lit :
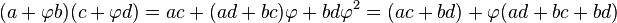
Ainsi les puissances de φ sont tous de la forme a + φ.b, plus précisément φn = un-1 + un.φ, où (un) désigne la suite de Fibonacci.
Ces deux anneaux possèdent des structures copie l'une de l'autre, le terme consacré pour décrire cette situation est celui d'isomorphisme. Un nombre réel de la forme a + φ.b est appelé un entier de Dirichlet. L'anneau des entiers de Dirichlet est le cadre naturel sous-jacent à toute l'arithmétique du nombre d'or. À certains égards, il est analogue à Z, l'ensemble des entiers naturels. Il est commutatif, et intègre. Le terme intègre signifie que si la multiplication de deux éléments α.β donne 0 alors soit α soit β est nul. La ressemblance est plus profonde, cet anneau est euclidien, c'est-à-dire qu'il dispose d'une division euclidienne semblable à celle de l'arithmétique des entiers classiques. Les outils de l'arithmétique usuelle sur Z, comme le théorème de Bachet-Bézout, le lemme d'Euclide, le théorème fondamental de l'arithmétique ou en plus sophistiqué le petit théorème de Fermat sont tous des conséquences de la division euclidienne. Elle offre des propriétés analogues pour l'arithmétique du nombre d'or. Cette analogie profonde pousse les arithméticiens à parler d'entiers pour décrire les éléments de cet ensemble. La compréhension de l'arithmétique de Z passe souvent par celles des nombres premiers. L'arithmétique du nombre d'or dispose aussi de ses nombres premiers de Dirichlet. Un nombre premier de Z n'est pas toujours premier dans l'arithmétique du nombre d'or, comme le montre le contre-exemple 19 :
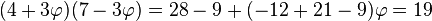
Cette différence engendre des modifications dans l'application des théorèmes classiques. Par exemple si p est un nombre premier différent de 5 tel que le reste de sa division euclidienne par 5 soit un carré parfait, donc égal à 1 ou à 4, le petit théorème de Fermat indique que φp-1 - 1 est un multiple de p. Ceci montre que up-1 est un multiple de p ainsi que up-2 - 1, en effet, φp-1 - 1 = up-2 - 1 + up-1.φ. Les démonstrations sont proposées dans l'article détaillé.