Nombre constructible - Définition

Introduction

Un nombre constructible à la règle et au compas est la mesure d'une longueur associée à deux points constructibles à la règle (non graduée) et au compas. Ainsi, est un nombre constructible, mais ni ni π ne le sont.

C'est du moins ainsi que le définissaient les mathématiciens grecs et tous ceux qui, à leur suite, ont cherché à déterminer quels étaient les points et les nombres constructibles de cette façon.

Du temps de la mathématique grecque, on distinguait les problèmes dont les solutions ne faisaient intervenir que des droites et des cercles dans le plan, de ceux faisant intervenir d'autres procédés (utilisation de courbes dites « mécaniques » telles la spirale d'Archimède ou les conchoïdes, utilisation de coniques pour les problèmes dits solides...). Cette distinction est à la source de problèmes célèbres comme la quadrature du cercle, la trisection de l'angle et la duplication du cube.

Les mathématiciens, jusqu'au XVII^e siècle n'accordaient aucune réalité concrète aux nombres négatifs. Il est cependant commode d'appliquer la définition, non seulement à des longueurs, mais également à des coordonnées de points constructibles.

Définition d'un nombre constructible

On donne ici une définition mathématique précise de la notion de point constructible (sous-entendu, à la règle et au compas). Remarquons que ni le vocabulaire intermédiaire introduit ni les notations ne sont classiques. On les a introduits pour décomposer proprement ce concept mathématique.

Points constructibles

Points constructibles en 1 étape

Soit E un sous-ensemble du plan euclidien, qu'on assimile ici à . On dit qu'un point P = (x,y) est constructible en 1 étape à partir de E si, et seulement si, P est un point de E ou si P est dans l'intersection de deux objets quelconques parmi :

• l'ensemble des droites qui passent par deux éléments distincts de E ;
• l'ensemble des cercles centrés en un point de E et dont le rayon est la distance de deux quelconques points de E.

On note C₁(E) l'ensemble des points constructibles en 1 étape à partir de E.

On peut remarquer que si E est fini, alors, C₁(E) l'est aussi.

Points constructibles en n étapes

Partant des mêmes données, on définit, naturellement et par récurrence, l'ensemble C_n(E) des points constructibles en n étapes à partir de E. Pour n = 1, c'est la construction précédente. Sinon, on pose : .

Points constructibles

Enfin, comme on s'y attend, l'ensemble des points constructibles à partir de E, qu'on note C(E), est la réunion (croissante) des C_n(E), c'est-à-dire : un point P est dit constructible à partir de E s'il existe n tel que P soit constructible en n étapes.

Nombres constructibles

On se place dans le même cadre, c'est-à-dire le plan euclidien assimilé à  ; on se donne E un sous-ensemble de .

Un nombre est dit constructible à partir de E s'il est l'abscisse d'un point constructible à partir de E.

Un nombre constructible est un nombre qui est constructible à partir de l'ensemble .

Opération sur les nombres constructibles

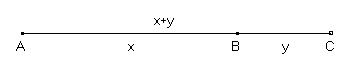
Addition

Soustraction

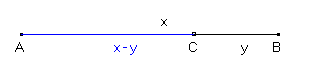
À condition que x > y

Multiplication

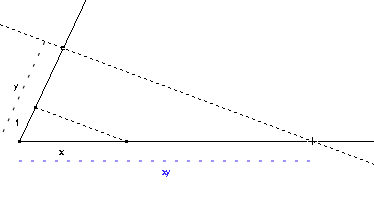
Une simple utilisation du théorème de Thalès permet de dire que 1×z = x × y

Division

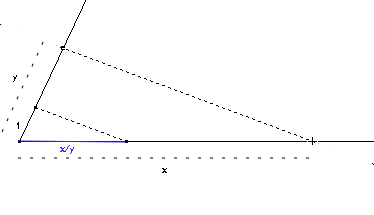
La même utilisation du théorème de Thalès permet de dire que

Ces observations permettent de dire que l'ensemble des nombres constructibles (si on accepte les distances négatives) est un corps commutatif. Les Grecs ont ainsi pu établir que tous les nombres rationnels positifs étaient constructibles. Mais leur première surprise est venue de la dernière opération.

Extraction de racine carrée

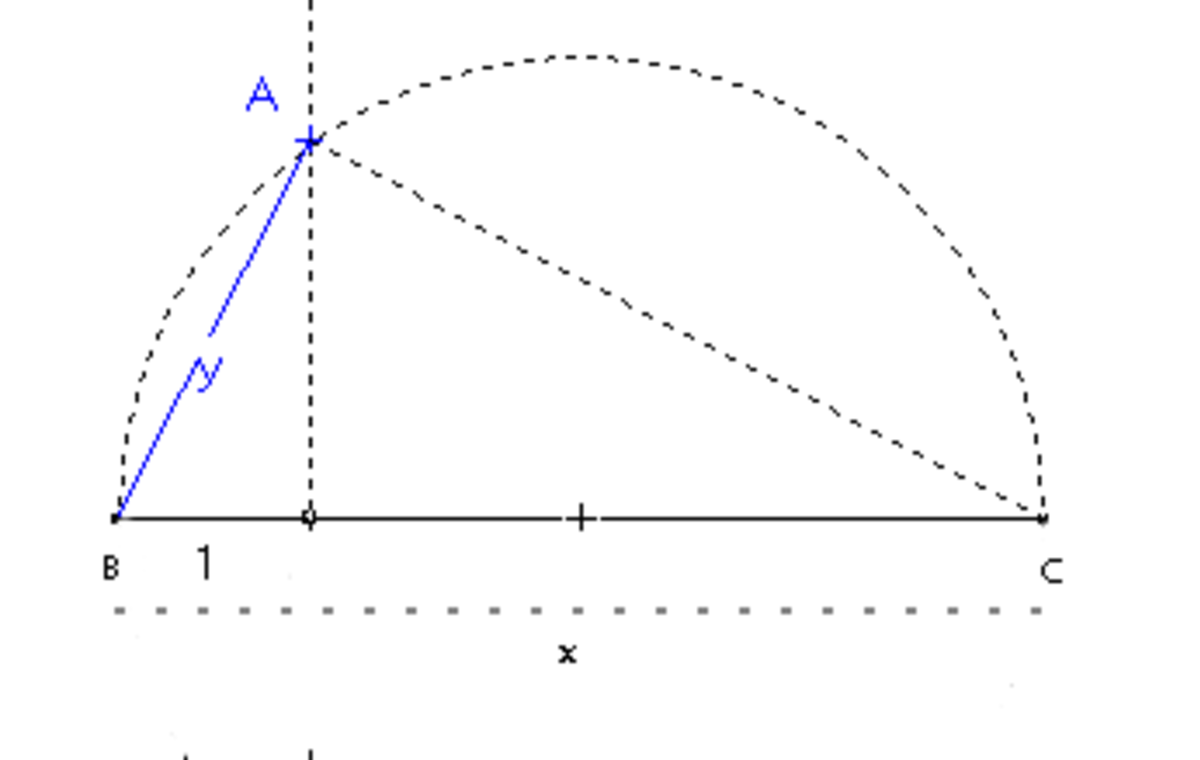
On utilise le fait que, dans un triangle rectangle en A, si H est le pied de la hauteur issue de A, on a

BH×BC = BA²

C'est une conséquence immédiate du fait que les triangles ABC et HAB sont semblables et de la propriété du triangle rectangle inscrit dans un demi-cercle.

On trace donc un segment [BC] dont la longueur correspond à la plus grande des valeurs entre x et 1, puis le cercle de diamètre BC, ensuite le point H sur [BC] tel que BH corresponde à la plus petite des valeurs entre x et 1, enfin la perpendiculaire à (BC) menée par H, qui rencontre le cercle en un point A. L'égalité  BA² = 1×x assure que

Les racines carrées sont donc constructibles.