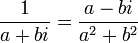Nombre complexe - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les nombres complexes forment une extension de l'ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels. Les nombres complexes furent introduits au XVIe siècle par les mathématiciens italiens Jérôme Cardan, Raphaël Bombelli, Nicolo Fontana, dit Tartaglia, et Ludovico Ferrari afin d'exprimer les solutions des équations du troisième degré en toute généralité par les formules de Cardan, en utilisant notamment des nombres de carré négatif, ainsi que les solutions des équations du quatrième degré (méthode de Ferrari).
L'ensemble des sommes et produits de nombres réels et du nombre imaginaire i (les nombres de la forme a + i.b) satisfait les propriétés d'une structure de corps commutatif qui contient le corps des réels. Il est appelé corps des nombres complexes et se note
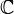
Ce n'est qu'à partir du XIXe siècle que se développe l'aspect géométrique des nombres complexes, vus comme des éléments ou des transformations du plan, sous l'impulsion de l'abbé Buée et de Jean-Robert Argand (plan d'Argand), puis avec les travaux de Gauss et de Cauchy.
En algèbre, le théorème de d'Alembert-Gauss identifie le degré d'un polynôme complexe non nul au nombre de ses racines comptées avec leur ordre de multiplicité. Le corps des nombres complexes est donc algébriquement clos.
En analyse, l'exponentielle complexe permet de simplifier l'étude des séries de Fourier puis de définir la transformée de Fourier. La branche de l'analyse complexe concerne l'étude des fonctions dérivables au sens complexe, appelées fonctions holomorphes.
En physique, les nombres complexes sont utilisés pour décrire le comportement d'oscillateurs électriques ou les phénomènes ondulatoires en électromagnétisme (Re(eiωt) représentant une onde).
Description
Notations des nombres complexes
Les nombres complexes, notés habituellement z, peuvent ainsi être présentés de plusieurs manières :
- forme cartésienne,
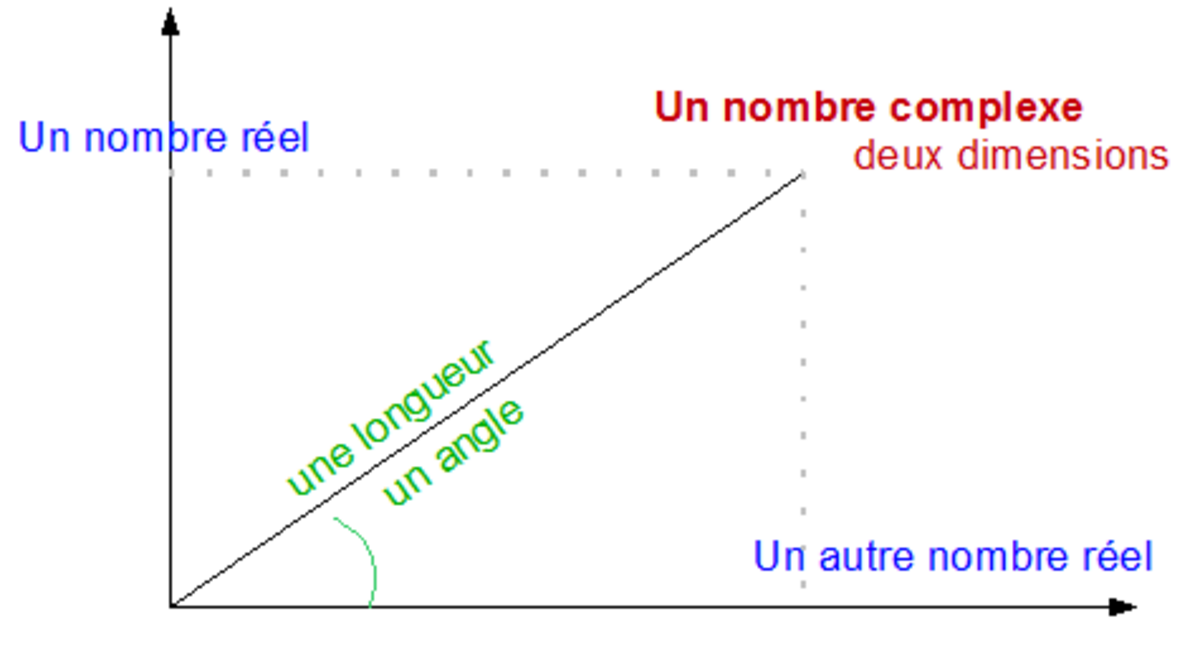
- algébrique :
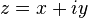
- ou vectorielle :
- algébrique :
- forme en coordonnées polaires :
- exponentielle
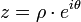
- ou vectorielle :
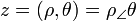
- ou trigonométrique :
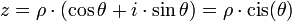
- exponentielle
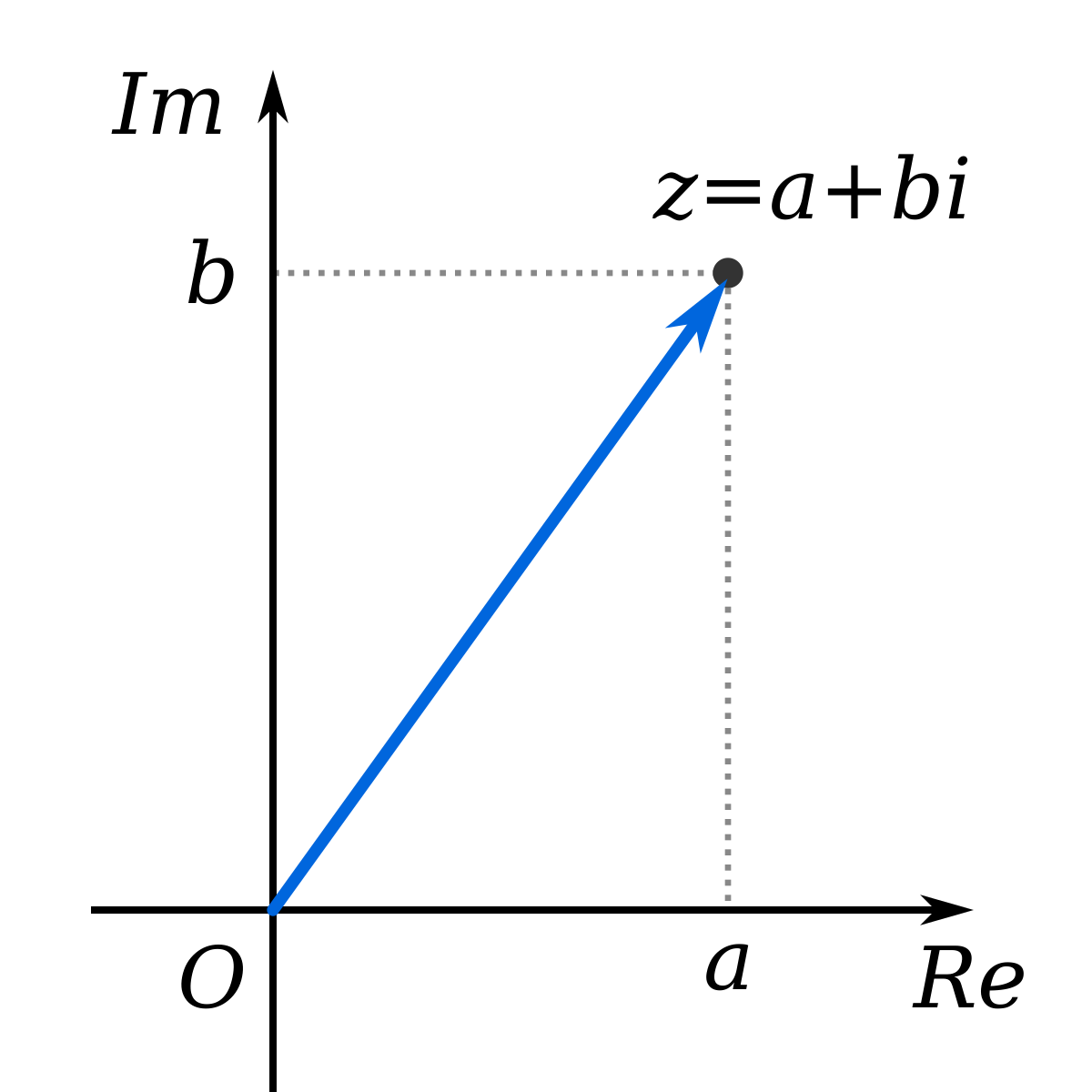
Forme cartésienne
Un nombre complexe
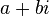
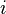
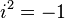
Le réel a est appelé partie réelle de z et se note
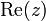
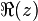
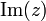
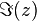
Deux nombres complexes sont égaux si et seulement s'ils ont la même partie réelle et la même partie imaginaire.
Un nombre complexe z est dit imaginaire pur ou totalement imaginaire si sa partie réelle est nulle, dans ce cas il s'écrit sous la forme z = bi. Un nombre complexe dont la partie imaginaire vaut 0 est assimilé à un nombre réel.
Le nombre réel 0 est le seul qui soit à la fois réel et imaginaire pur, mais la plupart des nombres complexes ne sont ni réels ni imaginaires purs.
L'addition et la multiplication sur les nombres complexes ont les mêmes propriétés d'associativité, de commutativité et de distributivité que sur les nombres réels. Les règles de calcul s'écrivent donc :
-
-
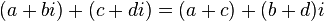
-
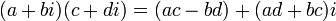
-
En particulier, cette formule permet d'obtenir l'égalité suivante :
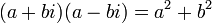
Puisque la somme a2+b2 de deux carrés de nombres réels est un nombre réel strictement positif (sauf si a = b = 0), il existe un inverse à tout nombre complexe non nul avec l'égalité :
Cette fraction fait apparaître deux expressions importantes pour le nombre complexe
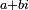
-
- son conjugué
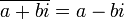
- son module
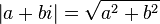
- son conjugué
L'application de conjugaison est un automorphisme involutif :
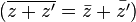
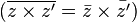
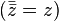
L'application module est une valeur absolue car elle est strictement positive en dehors de 0, sous-additive
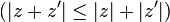
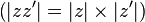
Les réels sont les seuls nombres complexes qui sont égaux à leur conjugué. Les réels positifs sont les seuls complexes égaux à leur module.
Le nombre 0 est le seul nombre complexe dont le module vaut 0.
Forme polaire
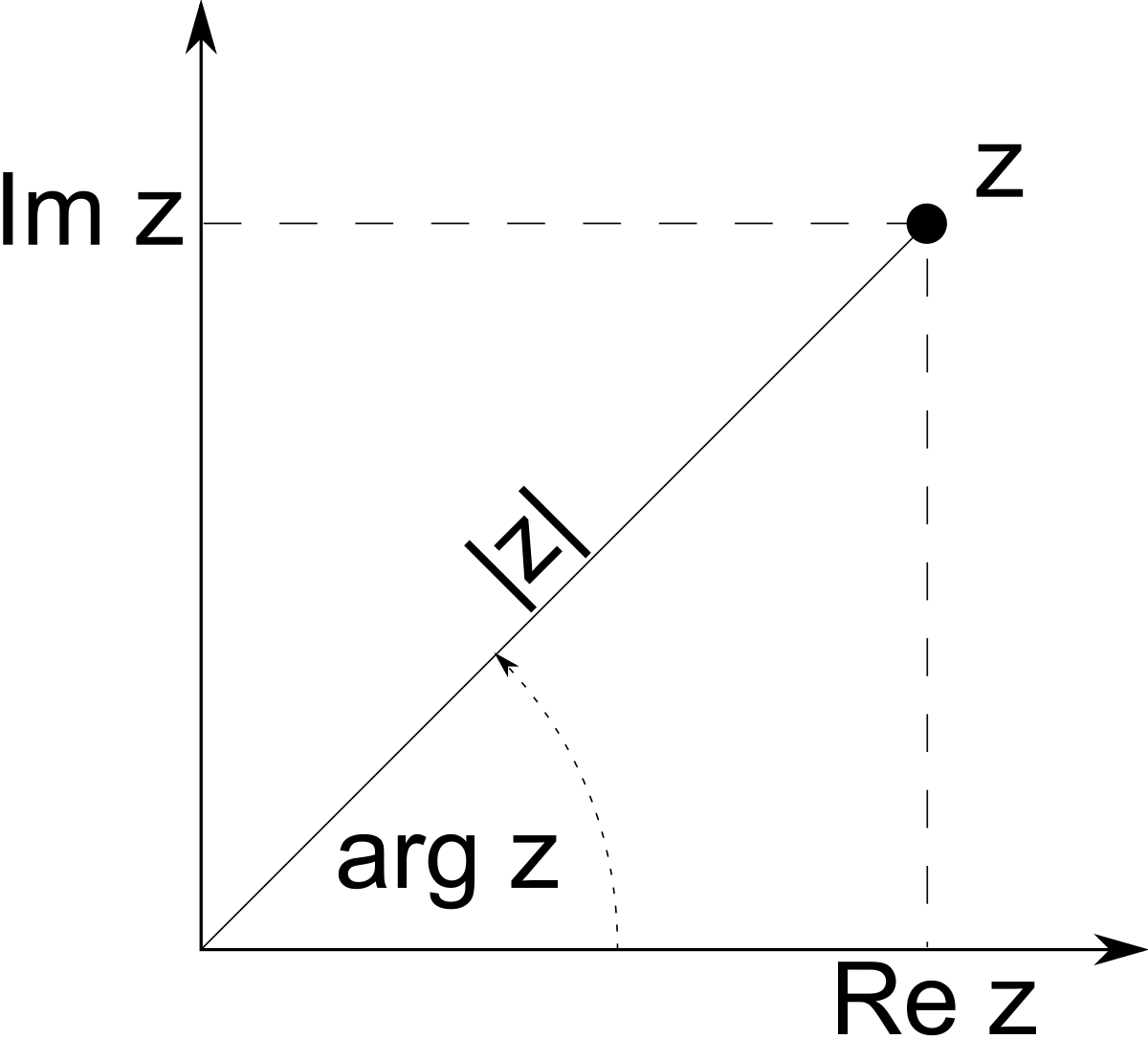
Plan complexe
Dans un plan affine
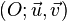
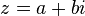
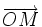
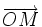
Le module
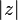
![\,\ [OM]](https://static.techno-science.net/illustration/Definitions/autres/5/5b716a48b43aa6b03064208c731a630b_e2d9a9d9758f4cbc53d7b0af6baa8755.png)
Si z est différent de 0, son image est distincte de l'origine O du repère. On appelle alors argument de z et on note
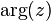
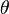
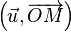
Par exemple, les réels strictement positifs ont un argument multiple de 2π, les réels strictement négatifs ont pour argument un multiple impair de π.
Les imaginaires purs non nuls ont un argument congru à
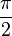
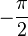
Le plan
Coordonnées polaires
Le module et l'argument d'un nombre complexe correspondent aux coordonnées polaires (r,θ) de son image dans le plan complexe. En écrivant les coordonnées cartésiennes à partir des coordonnées polaires, tout nombre complexe non nul peut donc s'écrire sous une forme trigonométrique
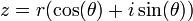
 .
.
La formule d'Euler
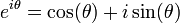
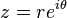
Le conjugué s'écrit alors simplement
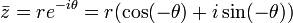
Cette écriture est en outre adaptée au calcul du produit de deux nombres complexes du fait des propriétés multiplicatives de la fonction exponentielle :
-
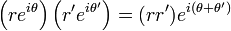
-
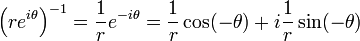
Interprétation géométrique des opérations
Soit z et z' deux nombres complexes d'images respectives M et M'.
- L'image
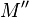
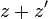
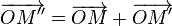
L'action d'un nombre complexe par addition s'interprète géométriquement comme une translation selon le vecteur image. - Soit λ un nombre réel, l'image M1 du produit
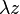
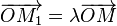
L'action du nombre réel λ par multiplication scalaire s'interprète géométriquement comme une homothétie de centre O et de rapport λ sur le plan complexe. - Si z est de module 1 et d'argument θ, l'image
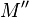
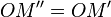
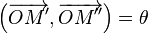
L'action d'un nombre complexe de module 1 par multiplication s'interprète géométriquement comme une rotation de centre l'origine et d'angle l'argument. - Par composition d'une homothétie et d'une rotation, l'action d'un nombre complexe z non nul par multiplication s'interprète géométriquement comme une similitude directe de centre l'origine, de rapport
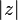
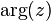
- L'image du conjugué
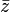
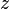
- L'image de l'inverse