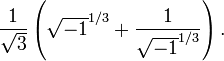Nombre complexe - Définition

Historique

Les nombres complexes apparaissent plus clairement au XVI^e siècle, quand est établie une formule de calcul pour les racines polynomiales des équations cubiques et quartiques polynomiales par les mathématiciens italiens Niccolo Fontana Tartaglia et Girolamo Cardano. On réalise très tôt que ces formules, même si l'on ne s'intéresse qu'aux solutions réelles, nécessitent parfois de manipuler la racine carrée de nombres négatifs. Par exemple, la formule cubique de Tartaglia donne la solution suivante à l'équation x³ − x = 0:

Le calcul formel avec les nombres complexes montre que l'équation z³ = i a pour solution −i, et . En substituant ces résultats dans et en simplifiant, on obtient 0, 1 et −1 comme solutions de x³ − x = 0.

Ces méthodes de calcul sont obtenues alors que la notion de nombre négatif n'est pas encore validée à l'époque. L'appellation nombre imaginaire pour ces quantités est introduite, tant leur réalité est contestable, par René Descartes en 1637. Une source de confusion supplémentaire réside dans le fait que l’équation combinée avec l'identité algébrique (valide avec des réels positifs a et b) aboutit au résultat absurde . L’utilisation incorrecte de cette identité (et de l’identité liée 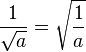) dans le cas où à la fois a et b sont négatifs tient notamment Leonhard Euler en échec. C’est cette difficulté qui mène les mathématiciens de l’époque à convenir d’utiliser le symbole spécial i à la place de pour se préserver de cette erreur.

Au XVIII^e siècle, en 1730, Abraham de Moivre énonce la formule bien connue qui porte son nom (formule de De Moivre) :

Peu de temps après, en 1748, Euler donne, quant à lui, la formule suivante (formule d'Euler) :

Ce n'est qu'en 1799 que l'existence des nombres complexes est complètement admise avec l’interprétation géométrique décrite par Caspar Wessel. Plusieurs années après, Carl Friedrich Gauss la redécouvre et la popularise et c'est alors que cette théorie prend un essor considérable. Il a noté cependant que l’idée d’une représentation graphique des nombres complexes est déjà mentionnée, en 1685, dans l’ouvrage de John Wallis De Algebra tractatus.

Un mémoire de Wessel, clair et complet, apparaît dans les minutes de l’Académie de Copenhague en 1799. Il y reconsidère la sphère et fournit une théorie des quaternions à partir de laquelle il développe une théorie complète sur la trigonométrie sphérique. Dans une publication de 1806, l’Abbé Buée reprend l’idée, suggérée par Wallis, que pourrait représenter 1 et -1 sur une ligne perpendiculaire à l’axe réel ; Jean-Robert Argand publie sur le même sujet au même moment. En 1831, Gauss établit une théorie relativement peu connue, et en 1832 publie son mémoire principal sur le sujet. On peut aussi mentionner le petit traité de Mourey (1828), dans lequel les fondements de la théorie des nombres directionnels sont posés. L’acceptation générale de la théorie doit aussi beaucoup aux travaux de Augustin Louis Cauchy et Niels Henrik Abel, ce dernier étant spécialement connu comme le premier à avoir fait, avec succès, un usage massif des nombres complexes.

La plupart des termes communément utilisés dans la théorie sont dus aux fondateurs :

• Argand appele cosφ + isinφ le facteur direction, et 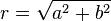le module ;
• Cauchy (1828) appelle cosφ + isinφ l'expression réduite ;
• Gauss utilise i pour 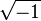, introduit le terme nombre complexe pour a + bi et appelle a² + b² la norme ;
• Hankel (1867) appelle cosφ + isinφ coefficient directionnel ;
• Weierstrass, quant à lui, emploie valeur absolue pour module.

Après Cauchy et Gauss suivront nombre de contributeurs. Parmi ceux-ci :

• Kummer (1844) ;
• Kronecker (1845),
• Scheffler (1845, 1851, 1880) ;
• Bellavitis (1835, 1852) ;
• Peacock (1845) ;
• De Morgan (1849) ;
• Möbius à qui l'on doit de nombreuses publications sur les applications géométriques des nombres complexes ;
• Dirichlet pour avoir étendu la théorie des nombres complexes et y incluant les nombres premiers, la notion de congruence, de réciprocité, etc., comme dans le cas des nombres réels.

Un anneau ou un corps est un ensemble de nombres stable par addition, soustraction et multiplication (et division dans le cas d'un corps. Gauss étudie les nombres complexes de la forme a + bi, où a et b sont entiers, ou rationnels. Son élève, Ferdinand Eisenstein, étudie les nombres de la forme a + bω, où ω est une racine complexe de x³ − 1 = 0. D’autres corps, dits cyclotomique, sont obtenus à partir des racines de l’unité x^k − 1 = 0 pour k entier positif quelconque. Cette généralisation est largement due à Kummer, qui invente aussi les nombres idéaux.

Enfin, parmi les derniers contributeurs (après 1884) de la théorie générale :

• Weierstrass ;
• Schwarz ;
• Dedekind ;
• Hölder ;
• l'abbé Berloty ;
• Poincaré ;
• Eduard Study ;
• MacFarlane.

Une définition formelle correcte, utilisant des paires de nombres réels, a été donnée au XIX^e siècle.