Nombre complexe - Définition

Développements en mathématiques

Analyse complexe

Les nombres complexes ont initialement été conçus pour répondre à un problème algébrique. Cependant, étendre les définitions de l'analyse au champ des nombres complexes s'avère tout aussi fécond. Par exemple la définition usuelle de la dérivée : (avec usage de la multiplication et de la soustraction complexes) permet d'obtenir une nouvelle notion de fonction dérivable, de variable complexe à valeurs complexes appelée fonction holomorphe. Cette notion s'avère plus restrictive que son pendant réel, notamment, toute fonction holomorphe voit sa dérivée être holomorphe, et même, toute fonction holomorphe est analytique, c'est-à-dire admet un développement en série entière en chacun des points de son domaine d'holomorphie.

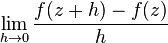
En théorie de l'intégration, en utilisant la notion d'intégrale le long d'un chemin, on obtient le théorème intégral de Cauchy, qui assure que l'intégrale d'une fonction holomorphe, sur un domaine vérifiant certaines propriétés topologiques, le long d'un chemin fermé, est nulle. Cette propriété cruciale permet d'obtenir la notion de primitive d'une fonction holomorphe, toujours sur un domaine adapté. Certaines de ces conditions topologiques peuvent être abandonnées, grâce à la notion de point singulier, aboutissant au théorème des résidus.

Représentations graphiques

Longtemps réputées non représentables graphiquement, les fonctions holomorphes ou de manière plus générale les fonctions complexes peuvent maintenant être représentées grâce aux découvertes récentes en informatique.

Dynamique holomorphe

La dynamique holomorphe à une variable consiste en l'étude du comportement des itérés d'une fonction holomorphe f définie sur une surface de Riemann. On distingue deux types de points sur ces surfaces : ceux où la famille des itérés est normale, en ces points la dynamique est assez simple (bassins d'attractions de cycles de points périodiques), dont l'ensemble est appelé ensemble de Fatou de f, puis ceux où le comportement est chaotique et dont l'ensemble est appelé ensemble de Julia de f.

Les propriétés de ces itérés sont particulièrement bien connues dans le cadre de la sphère de Riemann : classification complète des composantes connexes de l'ensemble de Fatou selon les propriétés de f, propriétés de l'ensemble de Julia, étude des espaces à paramètres de polynômes...

On étudie aussi la dynamique holomorphe à plusieurs variables, par exemple dans les espaces projectifs complexes où apparaissent de nouvelles difficultés par rapport à une variable telles que la présence d'ensembles de points où f n'est pas définie.

Équations différentielles dans le champ complexe

L'étude des équations différentielles holomorphes a les mêmes résultats de base que celle des équations sur des fonctions de variable réelle, et notamment le théorème de Cauchy-Lipschitz, qui donne l'existence et l'unicité d'une solution à un problème de Cauchy ; ou les résultats d'algèbre linéaire sur les espaces de solutions des équations différentielles linéaires.

Cependant, l'étude des équations aux points singuliers est nettement plus féconde que les simples études de raccord du cas réel : la topologie du plan complexe au voisinage d'un point singulier fait qu'il y a une infinité de manière de l'approcher, et l'étude des raccords des solutions obtenues avec toutes les méthodes d'approche amène à la notion de monodromie. Cette notion est ensuite utilisée dans un cadre plus général : la théorie de Galois différentielle.

Analyse de Fourier

Nombres hypercomplexes

En topologie

• En identifiant l'espace vectoriel avec l'espace vectoriel , la multiplication par définit une application sans point fixe sur les sphères de dimension impaire.
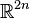
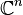
• L'adjonction d'un point « à l'infini » au plan complexe définit la sphère de Riemann homéomorphe à la sphère usuelle S², qui peut être vue comme le premier espace projectif complexe.
  La projection de la sphère S³, vue comme sphère unité de l'espace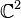 , sur la sphère de Riemann par quotient de l'action du cercle unité S¹ constitue alors la fibration de Hopf.
• Les espaces projectifs complexes de dimension paire engendrent rationnellement l'anneau de cobordisme orienté.