Nombre algébrique - Définition

Nombres définis par des radicaux

Tous les nombres qui peuvent être obtenus à partir des entiers en utilisant un nombre fini d'additions, de soustractions, de multiplications, de divisions et d'extractions de racines n-ièmes (où n est un nombre entier positif) sont algébriques. La réciproque, néanmoins, n'est pas vraie : il existe des nombres algébriques qui ne peuvent pas être obtenus de cette manière (c'est le théorème d'Abel–Ruffini); d'après la théorie de Galois, tous ces nombres sont de degré supérieur ou égal à  5. Un exemple d'un tel nombre est l'unique racine réelle de .

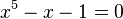
Classes particulières de nombres algébriques

• Entier de Gauss
• Entier d'Eisenstein
• Entier de Dirichlet
• Entier quadratique
• Entier algébrique
• Racine de l'unité
• Période de Gauss
• Nombre de Pisot-Vijayaraghavan
• Nombre de Salem

Généralisation

Plus généralement : soient un corps, et une extension de . Un élément de est dit algébrique sur s'il est racine d'une équation polynomiale à coefficients dans , non tous nuls ; il est dit transcendant sur dans le cas contraire.

La définition donnée plus haut s'obtient dans le cas particulier où est le corps des rationnels et est le corps des nombres complexes.