Multiplication - Définition
La liste des auteurs de cet article est disponible ici.
Notation
Dans les tablettes babyloniennes, il existe un idéogramme pour représenter la multiplication A - DU.
Dans les éléments d'Euclide, la multiplication est vue comme le calcul d'une aire. Ainsi, pour représenter le produit de deux nombres, on parle d'un rectangle ABCD, dans lequel les côtés AB et AD représentent les deux nombres. Le produit des deux nombres est alors appelé le rectangle BD (sous-entendu l'aire du rectangle de côtés AB et AD).
Diophante, lui, n'utilise pas de symbole spécial pour la multiplication, plaçant les nombres côte à côte. On retrouve cette même absence de signe dans les mathématiques indiennes, les nombres sont souvent placés côte à côte, parfois séparés par un point ou parfois suivis de l'abréviation bha (pour bhavita, le produit).
En Europe, avant que le langage symbolique ne soit définitivement admis, les opérations s'exprimaient en phrases écrites en latin. Ainsi 3 fois 5 s'écrivait-il 3 in 5.
Au XVIe siècle, on voit apparaître le symbole M utilisé par Stifel et Stevin. La croix de St André × est utilisée pour désigner une multiplication par Oughtred en 1631 (Clavis mathematicae). Mais on trouve à cette époque d'autres notations, par exemple une virgule précédée d'un rectangle chez Hérigone " 5 × 3" s'écrivant "☐ 5 , 3 :". Johann Rahn lui utilise le symbole * en 1659. Le point est utilisé par Leibniz qui trouve la croix trop proche de la lettre x. À la fin du XVIIe siècle, il n'existe toujours pas de signe établi pour la multiplication, Dans une lettre à Hermann, Leibniz précise que la multiplication n'a pas besoin de s'exprimer seulement par des croix mais que l'on peut utiliser aussi des virgules, des points ou des espaces .
Ce n'est qu'au cours du XVIIIe siècle que se généralise l'usage du point pour la multiplication dans le langage symbolique.
Techniques de multiplication
Excepté la multiplication égyptienne et sa variante russe qui utilisent un principe binaire, les techniques de multiplication qui se sont développées au cours des siècles, utilisent le système décimal et nécessitent pour la plupart de connaitre la table de multiplication des nombres de 1 à 9 ainsi que le principe de distributivité . Ainsi pour multiplier 43 par 25, on écrit que 43 × 25 = 43 ×(2 dizaines + 5 unités) . Ensuite, on distribue les différents termes
- 43 × 25 = 43 × 2 dizaines + 43 × 5 unités .
- 43 × 25 = (4 × 2 centaines + 3 × 2 dizaines) + (4 × 5 dizaines + 3 × 5 unités) = 8 centaines + 6 dizaines + 20 dizaines + 15 unités = 1075
Les différentes méthodes consistent à présenter ce calcul de manière pratique. On trouve ainsi la méthode chinoise qui commence par les poids forts, c'est-à-dire la multiplication des chiffres les plus à gauche. Celle méthode est celle utilisée dans la multiplication avec boulier. Mais d'autres méthodes sont possibles comme celle couramment utilisée dans les écoles françaises consistant à poser la multiplication en multipliant 43 d'abord par 5 puis par 2 dizaines et faire la somme.
| 4 | 3 | ||
| × | 2 | 5 | |
| 2 | 1 | 5 | |
| 8 | 6 | ||
| 1 | 0 | 7 | 5 |
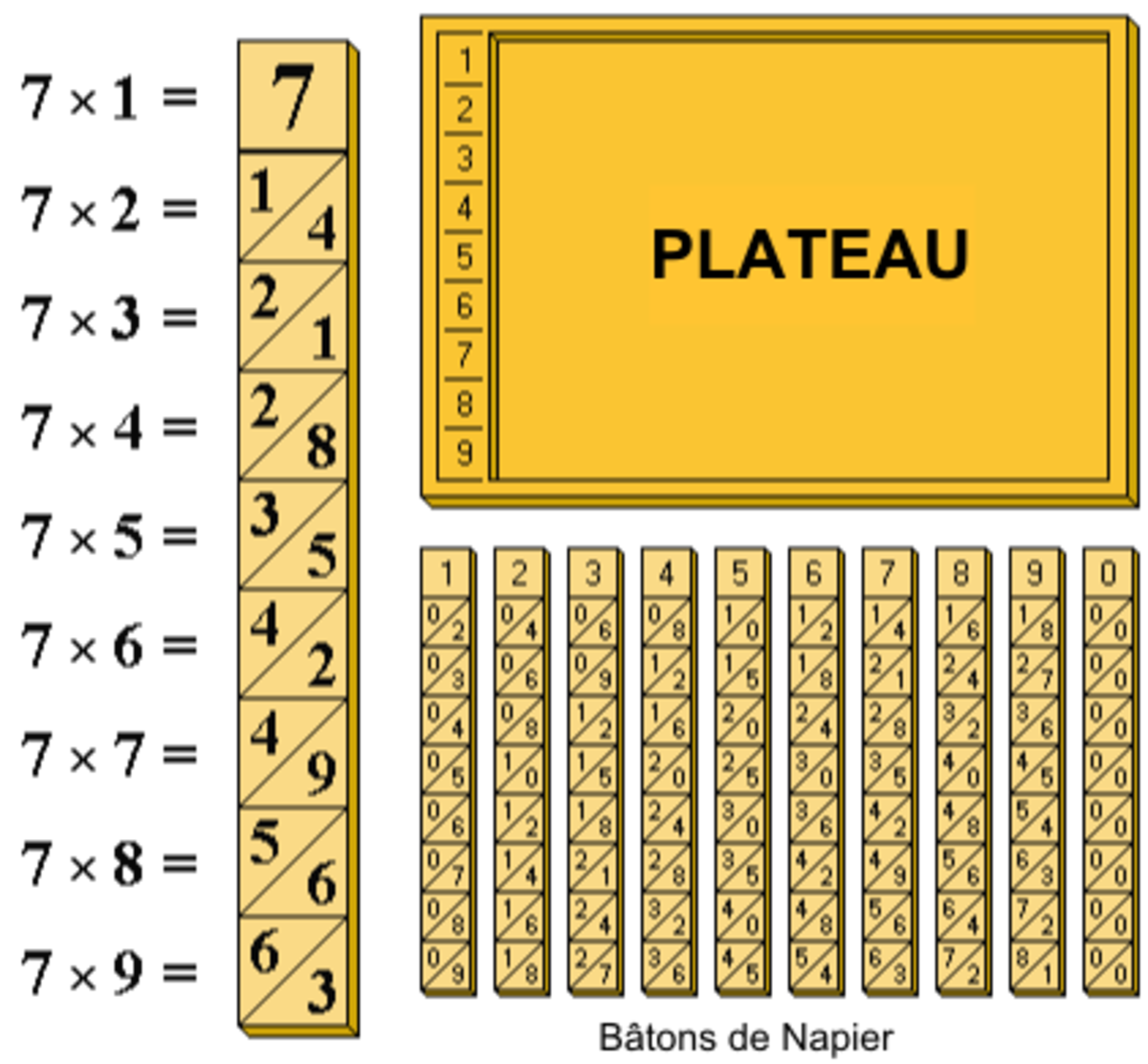
D'autres techniques utilisant ce même principe ont été développées comme la multiplication par glissement utilisée au IXe siècle par Al-Khawarizmi ou la multiplication par jalousies utilisée au Moyen Âge en Europe. Cette dernière a donné lieu à la fabrication de bâtons automatisant le calcul : les bâtons de Napier.
Ces techniques nécessitent pour la plupart la connaissance des tables de multiplication. Elle furent utilisées très tôt. On en trouve trace par exemple à Nippur en Mésopotamie 2000 ans avant J-C sur des tablettes réservées à l'entraînement des apprentis scribes.
La mémorisation des tables pour des nombres compris entre 6 et 9 se révèle parfois difficile. Georges Ifrah signale un moyen simple de multiplier avec les doigts des nombres compris entre 6 et 9. Sur chaque main, on dresse autant de doigts que d'unités dépassant 5 pour chacun des nombres concernés. Ainsi pour multiplier 8 par 7 on dresse 3 doigts de la main gauche et deux doigts de la main droite . La somme des doigts dressés donne le nombre de dizaines et le produit des doigts repliés donne le nombre d'unités à ajouter. Ainsi, dans l'exemple, il y a 5 doigts dressés donc 5 dizaines. Il y a 2 doigts pliés dans une main et 3 doigts pliés dans l'autre ce qui donne 2 × 3 = 6 unités soit 7 × 8 = 56.
L'explication mathématique fait appel encore une fois à la distributivité : si on appelle x et y le nombre de doigts repliés, les nombres de doigts dressés sont de a = 5 - x et b = 5 - y et on effectue la multiplication de 10 - x par 10 - y
- (10 - x)(10 - y) = 10(10 - x) - (10 - x) y = 10(10 - x ) - 10y + xy = 10 (10 - x - y) + xy = 10(a + b) + xy.
Une technique analogue existe pour multiplier entre eux des nombres compris entre 11 et 15. On ne se sert alors que des doigts dressés. Le nombre de doigts dressés donne le nombre de dizaines à ajouter à 100, et le produit des doigts dressés donne le nombre d'unités à ajouter.