Monoïde - Définition

Exemples

• L'ensemble des entiers naturels, muni de l'addition, est un monoïde, dont 0 est l'élément neutre ;
• L'ensemble des entiers naturels, muni de la multiplication, est un monoïde d'élément neutre 1. 0 n'est pas simplifiable  ;
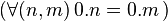
• L'ensemble des parties d'un ensemble E, muni de l'union ensembliste, est un monoïde, dont l'ensemble vide est l'élément neutre. Le même ensemble muni de l'intersection ensembliste est aussi un monoïde dont E est l'élément neutre.
• L'ensemble des entiers naturels muni de la loi Max qui a deux entiers associe le plus grand des deux est un monoïde de neutre 0.
• La deuxième loi d'un anneau possède une structure de monoïde. Beaucoup de propriétés des anneaux en découlent, notamment l'étude des Anneaux factoriels.

Symétrique d'un élément

• Soit (E, * ,e) un monoïde et soit x un élément de E. On dira que

1. x est symétrisable à droite si et seulement s'il existe un élément y dans E tel que x * y = e. On dit alors que y est un symétrique à droite de x.
2. x est symétrisable à gauche si et seulement s'il existe un élément z dans E tel que z * x = e. On dit alors que z est un symétrique à gauche de x.
3. x est symétrisable si et seulement si x est symétrisable à droite et à gauche.

• Lorsque x est symétrisable il admet un unique symétrique à droite et un unique symétrique à gauche et ceux-ci sont égaux. Cet unique élément est appelé symétrique de x.

En effet, c'est une conséquence de l'associativité, avec les notations ci-dessus y = e * y = (z * x) * y = z * (x * y) = z * e = z

• Le symétrique de x est généralement noté x ^{− 1}. On le note parfois lorsque la loi est commutative, c'est notamment le cas avec la multiplication des nombres réels. On le note − x lorsque la loi du monoïde est notée + .

Le symétrique est souvent appelé inverse, c'est notamment le cas pour les multiplications. Le symétrique pour les additions est appelé opposé.

• Si x et y sont symétrisables, il en est de même de x * y et on a (x * y) ^{− 1} = y ^{− 1} * x ^{− 1}.

On vérifie (x * y) * (y ^{− 1} * x ^{− 1}) = x * (y * y ^{− 1}) * x ^{− 1} = x * e * x ^{− 1} = x * x ^{− 1} = e grâce à l'associativité et on fait de même à gauche.

• L'ensemble des éléments symétrisables d'un monoïde forme un groupe.

Produit direct de monoïdes

• Soit et deux monoïdes. on peut munir le produit cartésien et d'une structure de monoïde en introduisant une nouvelle loi de la façon suivante :

.

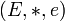
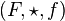
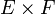
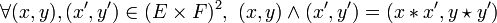
C'est un monoïde de neutre

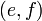
• Les deux projections de dans et de dans sont des morphismes de monoïde. Et le triplet vérifie la propriété universelle du produit direct.

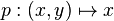
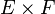
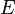
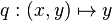
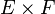
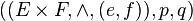
• Plus généralement, soit I un ensemble et une famille de monoïde. On construit la structure de produit direct sur le produit cartésien par la formule

.

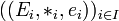
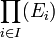
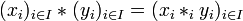
Applications

En mathématiques, il est rare d'utiliser les monoïdes ; car souvent, lorsqu'une structure est trop pauvre en termes de propriétés pour pouvoir continuer son étude, elle se trouve plongée dans une structure plus riche, comme les groupes, ou les anneaux... Les entiers naturels en sont un exemple frappant : pour les étudier, on étudie les entiers relatifs, qui eux forment un groupe, et mieux, un anneau factoriel !

En informatique théorique, les monoïdes et plus particulièrement le monoïde libre sont parmi les structures les plus utilisées, notamment dans la théorie des codes et dans la théorie des langages.