Méthode des moindres carrés - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Présentation de la méthode - Formalisme - Histoire - Robustesse - Interprétation statistique

Introduction

Illustration de la méthode des moindres carrés. Les données suivent la courbe figurée en pointillés et sont affectées par un bruit gaussien centré, de variance 1. Le meilleur ajustement déterminé par la méthode des moindres carrés est représenté en rouge.

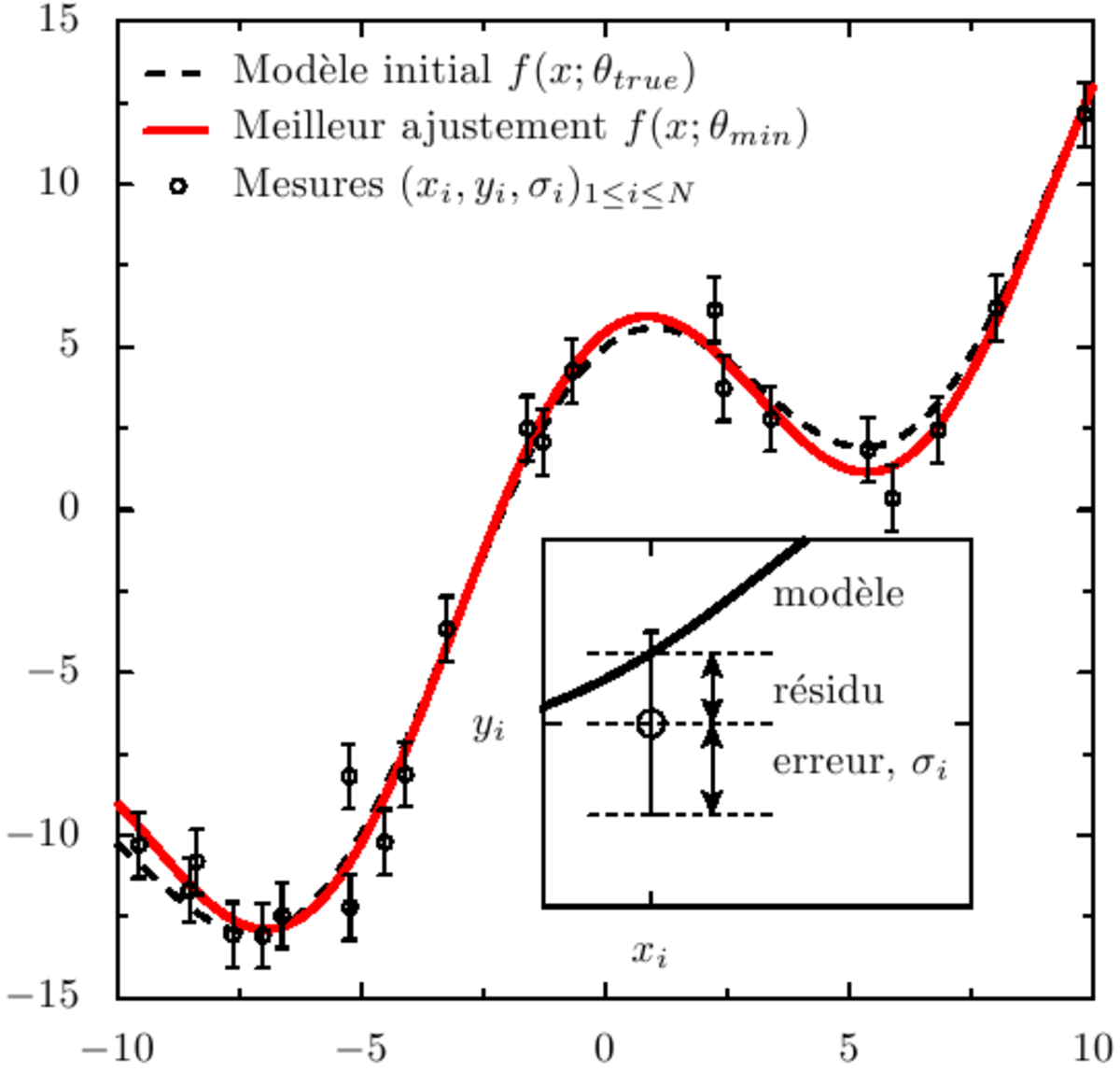
La méthode des moindres carrés, indépendamment élaborée par Legendre en 1805 et Gauss en 1809, permet de comparer des données expérimentales, généralement entachées d’erreurs de mesure, à un modèle mathématique censé décrire ces données.

Ce modèle peut prendre diverses formes. Il peut s’agir de lois de conservation que les quantités mesurées doivent respecter. La méthode des moindres carrés permet alors de minimiser l’impact des erreurs expérimentales en « ajoutant de l’information » dans le processus de mesure.

Présentation de la méthode

Dans le cas le plus courant, le modèle théorique est une famille de fonctions ƒ(x; $θ$ ) d’une ou plusieurs variables muettes x, indexées par un ou plusieurs paramètres $θ$ inconnus. La méthode des moindres carrés permet de sélectionner parmi ces fonctions, celle qui reproduit le mieux les données expérimentales. On parle dans ce cas d’ajustement par la méthode des moindres carrés. Si les paramètres $θ$ ont un sens physique la procédure d’ajustement donne également une estimation indirecte de la valeur de ces paramètres.

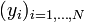
La méthode consiste en une prescription (initialement empirique), qui est que la fonction $f (x;θ)$ qui décrit « le mieux » les données est celle qui minimise la somme quadratique des déviations des mesures aux prédictions de $f (x;θ)$ . Si, par exemple, nous disposons de N mesures $(y_i)_{ i = 1,\ldots,N}$ , les paramètres $θ$ « optimaux » au sens de la méthode des moindres carrés sont ceux qui minimisent la quantité :

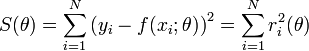
$S(\theta) = \sum_{i=1}^N \left(y_i - f(x_i;\theta)\right)^2 = \sum_{i=1}^N r^2_i(\theta)$

où les $r i (θ)$ sont les résidus au modèle, i.e. les écarts entre les points de mesure $y i$ et le modèle $f (x;θ)$ . $S (θ)$ peut être considéré comme une mesure de la distance entre les données expérimentales et le modèle théorique qui prédit ces données. La prescription des moindres carrés commande que cette distance soit minimale.

Si, comme c'est généralement le cas, on dispose d'une estimation de l'écart-type $σ i$ du bruit qui affecte chaque mesure $y i$ , on l'utilise pour « peser » la contribution de la mesure au χ². Une mesure aura d'autant plus de poids que son incertitude sera faible:

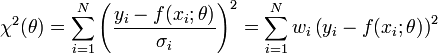
$\chi^2(\theta) = \sum_{i=1}^N \left(\frac{y_i - f(x_i;\theta)}{\sigma_i}\right)^2 = \sum_{i=1}^N w_i \left(y_i - f(x_i;\theta)\right)^2$

Les quantités $w i$ , inverses des variances des mesures sont appelés poids des mesures. La quantité ci-dessus est appelée khi carré ou khi-deux. Son nom vient de la loi statistique qu'elle décrit, si les erreurs de mesure qui entachent les $y i$ sont distribuées suivant une Loi normale (ce qui est très courant). Dans ce dernier cas, la méthode des moindres carrés permet de plus d’estimer quantitativement l’adéquation du modèle aux mesures, pour peu que l'on dispose d'une estimation fiable des erreurs $σ i$ . Si le modèle d’erreur est non gaussien, il faut généralement recourir à la méthode du maximum de vraisemblance, dont la méthode des moindres carrés est un cas particulier.

Son extrême simplicité fait que cette méthode est très couramment utilisée de nos jours en sciences expérimentales. Une application courante est le lissage des données expérimentales par une fonction empirique (fonction linéaire, polynômes ou splines). Cependant son usage le plus important est probablement la mesure de quantités physiques à partir de données expérimentales. Dans de nombreux cas, la quantité que l’on cherche à mesurer n’est pas observable et n’apparaît qu’indirectement comme paramètre $θ$ d’un modèle théorique $f (x;θ)$ . Dans ce dernier cas de figure, il est possible de montrer que la méthode des moindres carrés permet de construire un estimateur de $θ$ , qui vérifie certaines conditions d’optimalité. En particulier, lorsque le modèle $f (x;θ)$ est linéaire en fonction de $θ$ , le théorème de Gauss-Markov garantit que la méthode des moindres carrés permet d'obtenir l'estimateur non-biaisé le moins dispersé. Lorsque le modèle est une fonction non-linéaire des paramètres $θ$ l'estimateur est généralement biaisé. Par ailleurs, dans tous les cas, les estimateurs obtenus sont extrêmement sensibles aux points aberrants : on traduit ce fait en disant qu’ils sont non robustes. Plusieurs techniques permettent cependant de rendre plus robuste la méthode.