Méthode des moindres carrés - Définition
La liste des auteurs de cet article est disponible ici.
Histoire
Le jour du Nouvel An de 1801, l'astronome italien Giuseppe Piazzi a découvert l'astéroïde Cérès. Il a alors pu suivre sa trajectoire jusqu'au 14 février 1801. Durant cette année, plusieurs scientifiques ont tenté de prédire sa trajectoire sur la base des observations de Piazzi (à cette époque, la résolution des équations non linéaires de Kepler de la cinématique est un problème très difficile). La plupart des prédictions furent erronées; et le seul calcul suffisamment précis pour permettre à Zach, un astronome allemand, de localiser à nouveau Cérès à la fin de l'année, fut celui de Carl Friedrich Gauss, alors âgé de 24 ans (il avait déjà réalisé l'élaboration des concepts fondamentaux en 1795, lorsqu'il était alors âgé de 18 ans). Mais sa méthode des moindres carrés ne fut publiée qu'en 1809, lorsqu'elle parut dans le tome 2 de ses travaux sur la Mécanique céleste , Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium. Le mathématicien français Adrien-Marie Legendre a développé indépendamment la même méthode en 1805. Le mathématicien américain Robert Adrain a publié en 1808 une formulation de la méthode.
En 1829, Gauss a pu donner les raisons de l'efficacité de cette méthode ; en effet, la méthode des moindres carrés est justement optimale à l'égard de bien des critères. Cet argument est maintenant connu sous le nom du théorème de Gauss-Markov.
Robustesse
Sensibilité aux points aberrants
Techniques de robustification
Articles connexes
- La méthode des doubles moindres carrés
- Test du χ²
- Loi du χ²
- Apprentissage supervisé
- Simulation de profil
- M-estimateur
Interprétation statistique
Estimation statistique
Modèle standard: moindres carrés ordinaires
Pour le modèle matriciel
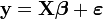
on conserve les hypothèses conventionnelles que
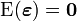
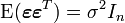
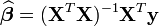
Une formalisation supplémentaire (on suppose par exemple en plus que les aléas sont normaux) permet d'obtenir les propriétés asymptotiques de l'estimateur:
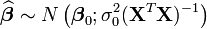
Les indices 0 indiquent qu'il s'agit de la vraie valeur des paramètres.
Moindres carrés généralisés
Lorsqu'on relâche (un peu) l'hypothèse sur la structure de la matrice de variance-covariance des erreurs, on peut toujours obtenir un estimateur par moindre-carré. On suppose donc que
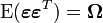
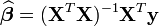
Les propriétés asymptotiques changent par rapport au cas standard:
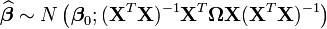
Moindres carrés pondérés
Si l'on connaît parfaitement la matrice de variance-covariance
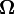
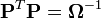
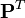
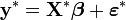
avec
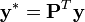
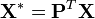
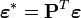
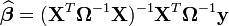
La distribution asymptotique sera:
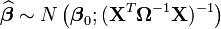
Le critère du χ²
Optimalité de la méthode des moindres carrés
Dans la régression linéaire classique,
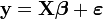
On suppose généralement que
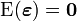
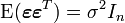
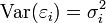
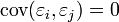
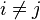
L'estimation par moindres carrés ordinaires (MCO) est
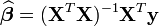
Sous les hypothèses précédentes, cet estimateur est connu pour être le meilleur estimateur linéaire sans biais (voir le Théorème de Gauss-Markov): cela signifie que parmi les estimateurs du type
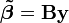
Enfin, si on suppose de plus que les aléas sont gaussiens, le modèle peut s'estimer par la Maximum de vraisemblance . Cet estimateur se trouve être celui par moindres carrés MCO et atteignant la borne de Cramer-Rao.
Enfin, sous les hypothèses du paragraphe sur les moindres carrés généralisés, l'estimateur reste BLUE.


















































