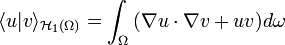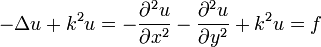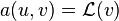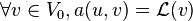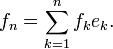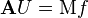Méthode des éléments finis - Définition
La liste des auteurs de cet article est disponible ici.
Méthode des éléments finis
Principe général
La méthode des éléments finis permet donc de résoudre de manière discrète une EDP dont on cherche une solution approchée « suffisamment » fiable. De manière générale, cette EDP porte sur une fonction u, définie sur un domaine. Elle comporte des conditions aux bords permettant d'assurer existence et unicité d'une solution.
Sauf cas particuliers, la discrétisation passe par une redéfinition et une approximation de la géométrie, on considère donc le problème posé sur la géométrie approchée par un domaine polygonal ou polyédrique par morceaux. Une fois la géométrie approchée, il faut choisir un espace d'approximation de la solution du problème, dans la MEF, cet espace est défini à l'aide du maillage du domaine (ce qui explique aussi pourquoi il est nécessaire d'approcher la géométrie). Le maillage du domaine permet d'en définir un pavage dont les pavés sont les éléments finis. Un élément fini est la donnée d'une cellule élémentaire et de fonctions de base de l'espace d'approximation dont le support est l'élément, et définies de manière à être interpolantes (voir Fonctions_de_base).
Bien qu'il existe de nombreux logiciels exploitant cette méthode et permettant de « résoudre » des problèmes dans divers domaines, il est important que l'utilisateur ait une bonne idée de ce qu'il fait, notamment quant au choix du maillage et du type d'éléments qui doivent être adaptés au problème posé : aucun logiciel ne fera tout pour l'utilisateur, et il faut toujours garder un œil critique vis-à-vis de solutions approchées. Pour cela il existe des indicateurs d'erreur et des estimateurs d'erreur qui permettent d'ajuster les différents paramètres.
La solution trouvée, il reste cependant à déterminer les caractéristiques de la méthode ainsi développée, notamment l'unicité de l'éventuelle solution ou encore la stabilité numérique du schéma de résolution. Il est essentiel de trouver une estimation juste de l'erreur liée à la discrétisation et montrer que la méthode ainsi écrite converge, c’est-à-dire que l'erreur tend vers 0 si la finesse du maillage tend elle aussi vers 0.
Dans le cas d'une EDP linéaire avec opérateur symétrique (comme l'est Δ), il s'agit finalement de résoudre une équation algébrique linéaire, inversible dans le meilleur des cas.
Dimensions
On développe ici la méthode des éléments finis en deux dimensions à valeurs réelles. On suppose que les équations étudiées sont des équations différentielles d'ordre deux.
La méthode est généralisable à des cadres d'espaces de dimension différente ou pour des équations aux dérivées partielles d'ordre supérieur :
- on traite ici le cas d'une solution réelle à une EDP, les cas où la dimension de la solution serait plus grande se traitent de façon similaire mais nécessitent des écritures plus complètes ; les cas les plus couramment rencontrés sont la dimension 1 (comme ici), 2 ou 3 (pour des problèmes de mécanique), 6 ou 12 (pour des problèmes d'électromagnétisme « réels ou complexes » respectivement) ;
- les degrés de différentiation supérieurs sont ramenés à un degré moindre par la méthode classique de réduction de degré : on fait intervenir des variables supplémentaires, c'est-à-dire des dérivées partielles des variables de départ (exemple classique : les EDP de la mécanique statique des poutres font intervenir la dérivation partielle d'ordre 4) ; il est parfois possible, pour des degrés supérieurs, d'appliquer plusieurs fois les méthodes de formulation variationnelles afin d'obtenir des ordres plus faibles — en tout cas lorsque le degré de dérivation est pair.
Bien que théoriquement la méthode soit transposable en dimensions supérieures du support, techniquement la complexité de création des discrétisations croît avec la dimension… et pratiquement, on résout rarement des problèmes en dimension supérieures à 3 — y compris des problèmes de dynamique en espace à 3 dimension qui pourraient être traité en quatre dimensions mais sont traités en réalité avec une méthode mixte éléments finis « en espace »/différences finies « en temps ».
Cadre algébrique, analytique et topologique
Soit un domaine (ouvert borné et connexe) Ω de
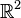
Soient les fonctions de Ω dans

Soient les applications continues sur Ω et différentiables sur Ω, de carré sommables sur Ω et de gradient de carré sommable sur Ω (ou de dérivées partielles de carré sommable, ce qui revient au même avec le support de dimension finie). Nommons cet espace
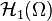
On note
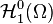
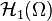
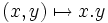
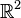
Cas organique
Hypothèses
On considère ƒ une fonction continue sur Ω de carré sommable et u la solution de l'équation aux dérivées partielles suivante sur Ω :
Avec la condition au bord u = 0 sur δΩ. Ceci peut également se réécrire u ∈ V0. Cette condition au bord s'appelle la condition de Dirichlet.
On démontre qu'il existe une solution unique à ce problème d'EDP à l'aide du théorème de Lax-Milgram.
Formulation faible
Soit v ∈ V0 quelconque. Multiplions les deux parties de l'équation précédente par v puis sommons sur le domaine Ω, puisque v et ƒ sont tous deux de carré sommable sur ce domaine. On obtient l'équation :
-
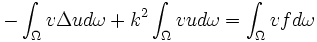
On utilise pour le premier terme une intégration par parties :
-
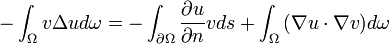
Dans cette formulation, v est nulle sur le bord (v ∈ V0) ce qui permet d'obtenir la formulation faible du problème :
-
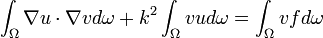
Si u est deux fois différentiable, il y a équivalence entre cette formulation et celle du problème initial donné dans la section hypothèse et alors la solution de la formulation faible est la même que la solution initiale. On peut donc résoudre la formulation faible au lieu de résoudre le problème initial.
La question de savoir s'il y a équivalence entre la formulation faible et la formulation initiale donnée dans les hypothèses peut être particulièrement délicate dans les cas limites où l'ouvert Ω n'est pas suffisamment régulier (par exemple s'il y a des points singuliers) ou si ƒ n'est pas suffisamment dérivable (si l'on ne suppose pas que ƒ est au moins
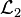
Notations et cadre général
Pour plus de généralité et pour rendre la suite plus lisible on utilisera les notations suivantes :
-
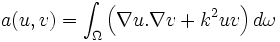

-
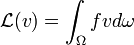
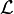

On peut résoudre par la méthode des éléments finis toute équation aux dérivées partielles dont la forme faible se met sous la forme
On montre que a un opérateur bilinéaire coercif continu selon la norme
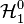
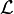
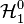
Puisque k>0, le théorème de Lax-Milgram assure l'existence de la solution et montre que u, solution du problème précédent, u est la solution unique du problème d'optimisation de la fonctionnelle suivante :
-
Cette égalité peut avoir un sens physique notamment du point de vue de l'énergie pour certaines équations physiques et peut servir à montrer l'existence et l'unicité de la solution grâce aux propriétés de a et de
Choix d'un maillage et Discrétisation
Choix d'un maillage
La méthode des éléments finis repose sur un découpage de l'espace selon un maillage. D'habitude l'on choisit un maillage carré ou triangulaire mais rien n'interdit de choisir des maillages plus complexes. Il n'est pas non plus nécessaire que le maillage soit régulier et l'on a tendance à resserrer le maillage près des endroits d'intérêts (par exemple aux endroits où l'on pense que la solution va beaucoup varier), cependant il faut veiller à avoir des éléments faiblement distordus (se rapprocher d'un polygone régulier). Plus ce maillage est resserré plus la solution que l'on obtient par la méthode des éléments finis sera précise et proche de la « vraie » solution de l'équation aux dérivés partielles.
Fonctions de base
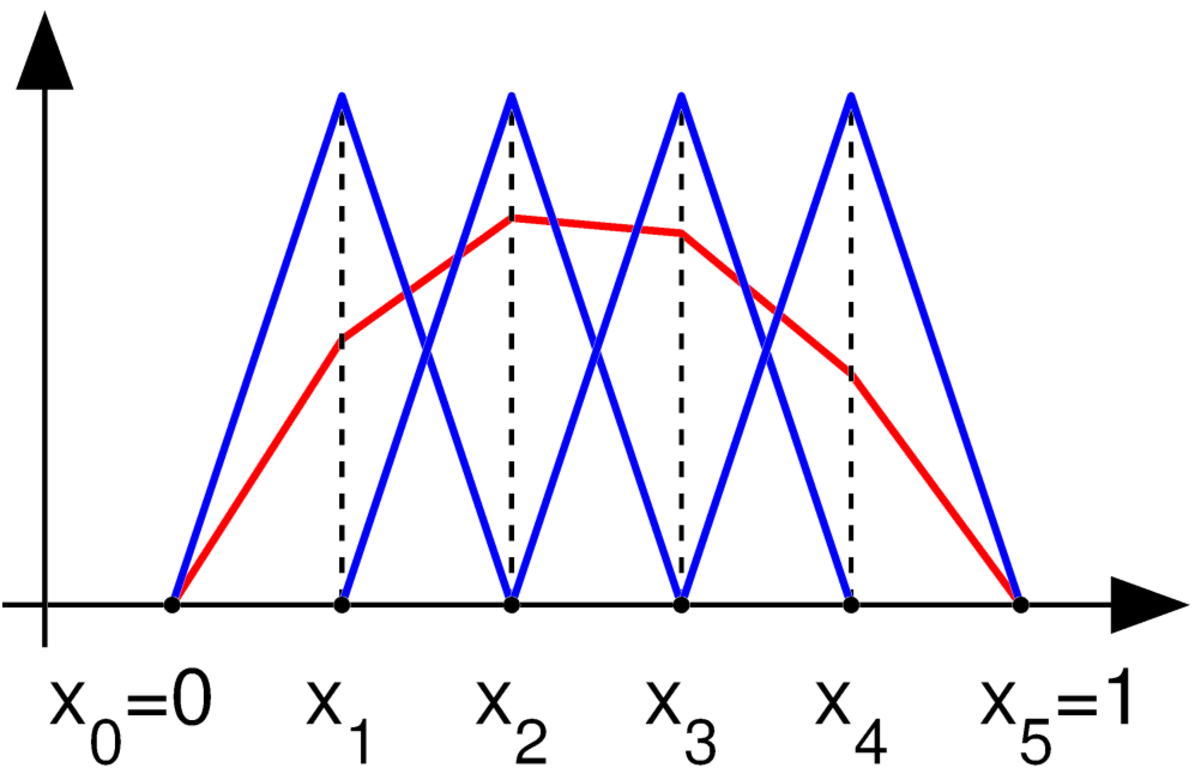
On doit après prendre une base de fonctions « adaptées » au maillage. Plusieurs choix sont alors possibles. En général, les fonctions de bases utilisées pour les éléments finis sont interpolantes, c'est-à-dire que les valeurs nodales sont les valeurs des grandeurs inconnues aux nœuds.
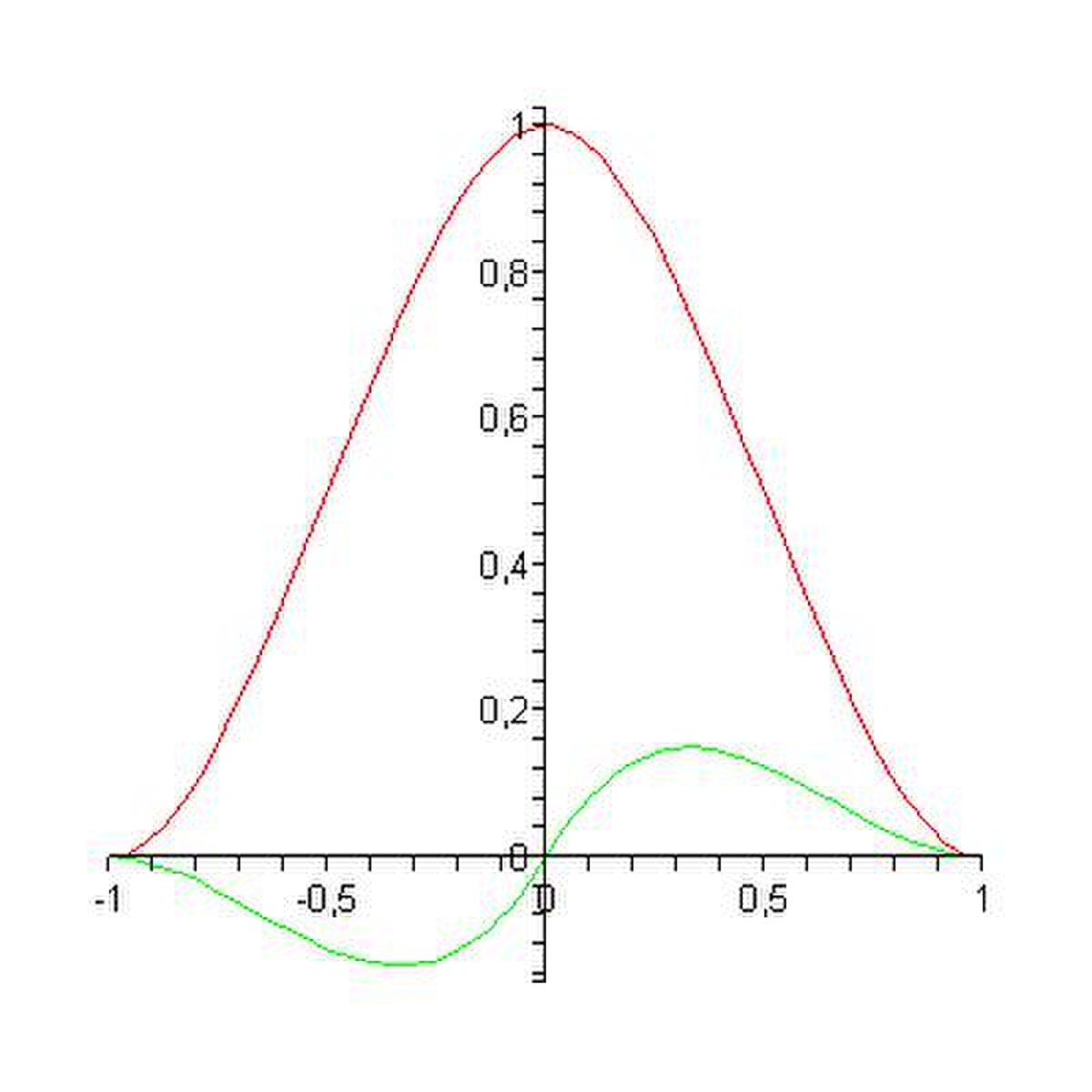
La plus simple est l'emploi des polynômes de Lagrange. Dans cette méthode les fonctions de base valent 1 à un nœud du maillage et 0 a tous les autres. La fonction de base i est alors la fonction valant 1 au nœud i et 0 sur les autres nœuds et qui est polynomiale sur chaque élément. Un exemple de telles fonctions est représenté en dimension 1 à côté. Il y a autant de fonctions de base par éléments que de nombre nœuds.
On appelle élément la donnée d'une géométrie (souvent polygonale en 2D, polyédrique en 3D) et de fonctions de bases associées à cette géométrie.
D'autres solutions peuvent exister pour les fonctions de base. On cite ici un seul exemple les éléments finis d'Hermite qui ont la particularité d'avoir deux fonctions de base associées à chaque nœud. Dans cette version, la valeur de la solution est ajustée avec la première fonction alors que la deuxième permet d'ajuster la valeur de la dérivée. Ce type de fonctions de base peut avoir un intérêt pour la résolution de certaines équations aux dérivées partielles (par exemple l'équation des plaques en mécanique des milieux continus) même si elle nécessite d'avoir deux fois plus de fonctions pour un maillage donné.
Quelques éléments classiques
- En 2D
- triangles de degré 1, (triangles à 3 nœuds, fonctions linéaires)
- triangles de degré 2 (triangles à 6 nœuds, polynômes de degré 2)
- quadrangles de degré 1 (carrés à quatre nœuds, fonctions linéaires)
- quadrangles de degré 2 (carrés à 8 ou 9 nœuds, polynômes de degré 2)
- En 3D
Discrétisation
Soit le maillage
On cherche la solution
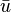
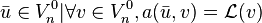
Or dans cet espace discrétisé, dire que tout vecteur vérifie la proposition précédente est équivalent à dire que tous les vecteurs de la base vérifient la proposition. Si l'on décompose la solution
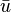
![\forall j \in [1,...,n] \sum_{i =1}^n { u_i a( e_i, e_j ) } = \mathcal{L}(e_j)](https://static.techno-science.net/illustration/Definitions/autres/9/912c1dec423a8ba2782262aa9c96a0d4_8451c46b5121c6b5988175a1be42e046.png)
L'idée est que quand le maillage se resserre et que le nombre de fonctions de base n tend vers l'infini (et que l'espace engendré par cette base
Éventuelle deuxième discrétisation
Dans certains problèmes physiques, il peut être intéressant de discrétiser une deuxième fois. Cette seconde discrétisation n'est pas nécessaire pour la méthode des éléments finis. Souvent on a comme expression de
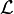
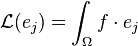
On projette alors f sur la base b. On obtient:
et on approche
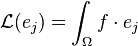
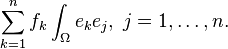
Le problème est d'obtenir ensuite une projection fn acceptable sachant qu'il n'y a pas nécessairement de produit scalaire associé à la base qui permette de projeter de façon efficace. Dans les deux exemples de bases donnés plus haut, cette projection est aisée. Dans le cas des éléments finis de Lagrange, la projection sur la fonction ei est donnée par la valeur en xi, dans le cas des éléments d'Hermite, c'est la valeur de la fonction ainsi que de sa dérivée qui permettent d'obtenir la projection. Pour d'autres bases, la projection peut être plus compliquée.
Problème sous forme matricielle
Si l'on note:
- la matrice A ayant pour composantes les a(ei,ej),
- le vecteur U ayant pour composantes les ui qui sont les coordonnées de la solution approché sur la base b
- le vecteur B pour composantes les
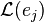
alors ce problème revient à résoudre l'équation linéaire de n équations à n inconnues :
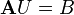
La matrice A est appelée matrice de rigidité par analogie avec certain problèmes de mécanique des solides. A est par construction symétrique, et puisque a est coercitive, alors A est symétrique, définie positive donc inversible. On obtient donc l'existence et l'unicité de U = A − 1B. grâce aux coordonnées de
Pour le cas avec une deuxième discrétisation de
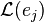
où M est appelée la matrice de masse et contient les
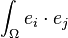
Algorithme
La méthode des éléments finis doit être conduite ainsi
- On calcule la matrice de rigidité A
- On détermine le membre de droite, en calculant les termes
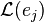
- On résout le problème AU=B ou le problème AU=Mf suivant le niveau de discrétisation choisi. U est alors donné par U = A − 1B. Selon la base qui a été choisie et selon les données du problème, il faut choisir la méthode d'inversion la plus efficace pour A. C'est l'étape la plus consommatrice en termes de puissance de calcul et l'efficacité de la méthode en termes de temps de calcul se joue principalement sur cette étape.
- On peut écrire
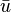
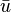
Condition de Neumann
La condition qui suit est très différente de celle de Dirichlet. On pose comme condition au bord que la dérivée normale existe sur le bord
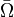
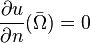
Si la fonction est supposée différentiable au bord
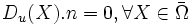
 .
.
Le résultat fonctionne de la même manière car l'élément clef de la démonstration où intervient l'hypothèse de bord est que l'intégrale
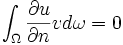
Par la suite, la différence réside surtout dans le choix des vecteurs de base pour la discrétisation : il faut conserver les fonctions tests propres aux nœuds du bord.