Mésomérie - Définition

Conception des mésomères

Doublets électroniques en chimie

Dans les systèmes conjugués, on parle de mésomérie lorsque dans une structure de Lewis, on a par exemple:

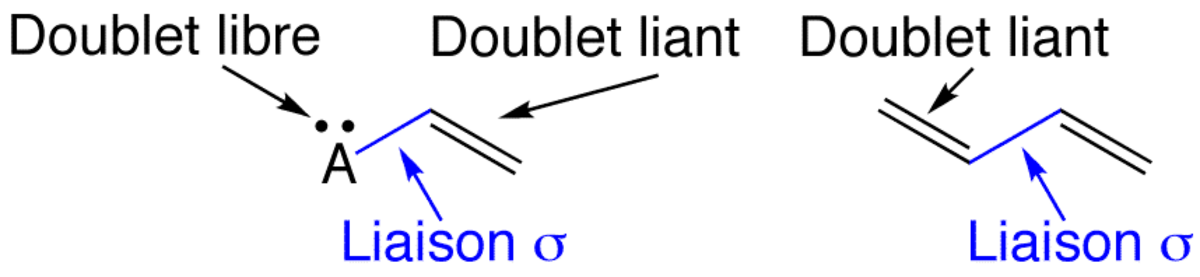
• une alternance doublet liant (π) - liaison simple (σ) - doublet liant (π), comme dans un diène conjugué,
• une alternance doublet libre - liaison simple (σ) - doublet liant (π), comme dans un éther vinylique,
• un couple doublet libre - liaison simple (σ) - orbitale p vide, comme dans le borazole (B₃N₃H₆),
• un couple doublet liant (π) - liaison simple (σ) - orbitale p vide, comme dans l'ion allyle (CH₂=CH-CH₂⁺),
• une alternance électron libre - liaison simple (σ) - doublet liant (π), comme dans le radical benzyle,

On passe d'une forme mésomère à une autre en utilisant une flèche courbée pour indiquer le déplacement d'un doublet d'électrons (libre ou liant) ou par une cascade de telles flèches, ou des demi-flèches indiquant le déplacement d'un seul électron dans le cas des radicaux, pour établir ou défaire des liaisons π. Les exemples ci-bas sont illustratifs. La séquence des flèches n'est pas importante. Toutefois, la mésomérie impose de ne casser aucune liaison σ (sigma) pour passer d'une forme à une autre. Dans le cadre de la mésomérie, les liaisons σ peuvent être vues comme définissant un squelette sur lequel se déplacent les électrons π.

L'importance de la contribution de chaque mésomère à la structure réelle peut varier, puisque certaines formulations seront nécessairement plus énergétiques, à cause d'un nombre inférieur de liaisons chimiques par exemple, et donc moins probables que d'autres. On considère alors que certaines structures seront « majoritaires » et d'autres « minoritaires » et que la structure réelle sera une moyenne pondérée de toutes les structures contribuantes, mais ressemblant plus aux structures « majoritaires » et moins aux autres. On attribue donc aux formes mésomères une « probabilité » ou « poids », selon certaines caractéristiques. Contribueront plus les mésomères qui:

• respectent le plus possible la règle de l'octet (on préfère avoir 8 électrons autour de chaque atome plutôt que des lacunes ou des hypervalences),
• sont dotés d'un minimum de charges électriques (on préfère une structure entièrement neutre à une structure faisant apparaître une séparation de charge +/-),
• placent les charges électriques sur les atomes les plus aptes à les soutenir (une charge négative sur un atome électronégatif et réciproquement).

La structure réelle est alors une combinaison linéaire de ces structures contribuantes, dont l'apport de chacune est évalué de manière qualitative selon ces caractéristiques et qui s'apparente à sa stabilité.

Rapport avec la stabilité

La mésomérie est une figuration de la délocalisation qui peut servir à expliquer ce qu'une seule formule de Lewis ne peut pas expliquer, mais elle n'explique pas le pourquoi de la délocalisation. Quand une mésomérie est nécessaire pour expliquer quelque chose, on est porté à croire que la mésomérie est stabilisante. En effet, la règle générale veut, que pour un type d'espèce chimique donné, que l'espèce avec plus de mésomères sera plus stable qu'une autre avec moins de mésomères. Mais cette règle ne permet pas de comparer un mésomère « majoritaire » avec un « minoritaire », et il est impossible de quantifier la stabilisation. Bien que l'on peut concevoir de « poids » relatifs pour chaque forme majoritaire or minoritaire, on ne peut pas représenter ces poids, et la mésomérie ne précise pas non plus la distribution électronique de la structure hybride.

La théorie des orbitales moléculaires permet la quantification de la stabilisation qui résulte d'une délocalisation, de visualiser et de préciser la distribution électronique résultante, ainsi que de mesurer les distances et angles interatomiques. Le mélange d'orbitales atomiques par recouvrement dans l'espace créent des orbitales dites moléculaires, liantes, non-liantes et anti-liantes, qui expliquent non seulement les liaisons π (et autres), mais aussi la stabilisation par conjugaison. Cette théorie peut aussi décrire l'hyperconjugaison, ce que les formes mésomères traduisent avec difficulté.