Meilleure réponse - Définition

Introduction

En théorie des jeux, la meilleure réponse est la stratégie ou l'ensemble de stratégies qui produisent le résultat immédiat le plus favorable au joueur considéré, étant données les stratégies des autres joueurs. Le concept de meilleure réponse est au centre de la notion d'équilibre de Nash (voir aussi John Forbes Nash) qui repose sur la sélection par chaque joueur et à chaque période de sa meilleure réponse.

Fonction de meilleure réponse

Fig. 1 - Fonction de meilleure réponse pour le joueur Y dans le jeu de la chasse au cerf.

La fonction de meilleure réponse (souvent notée ) est employée dans la preuve de l'existence d'équilibres de Nash en stratégies mixtes. Pour chaque joueur, on construit une fonction de l'ensemble des profils de stratégies de l'adversaire vers l'ensemble des stratégies du joueur considéré. Ainsi, pour tout ensemble donné de stratégies σ _{− i} de l'adversaire, b_i(σ _{− i}) représente les meilleurs réponses du joueur i à σ _{− i}.

Fig. 2 - Fonction de réaction pour le joueur X dans le jeu de la chasse au cerf.

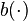
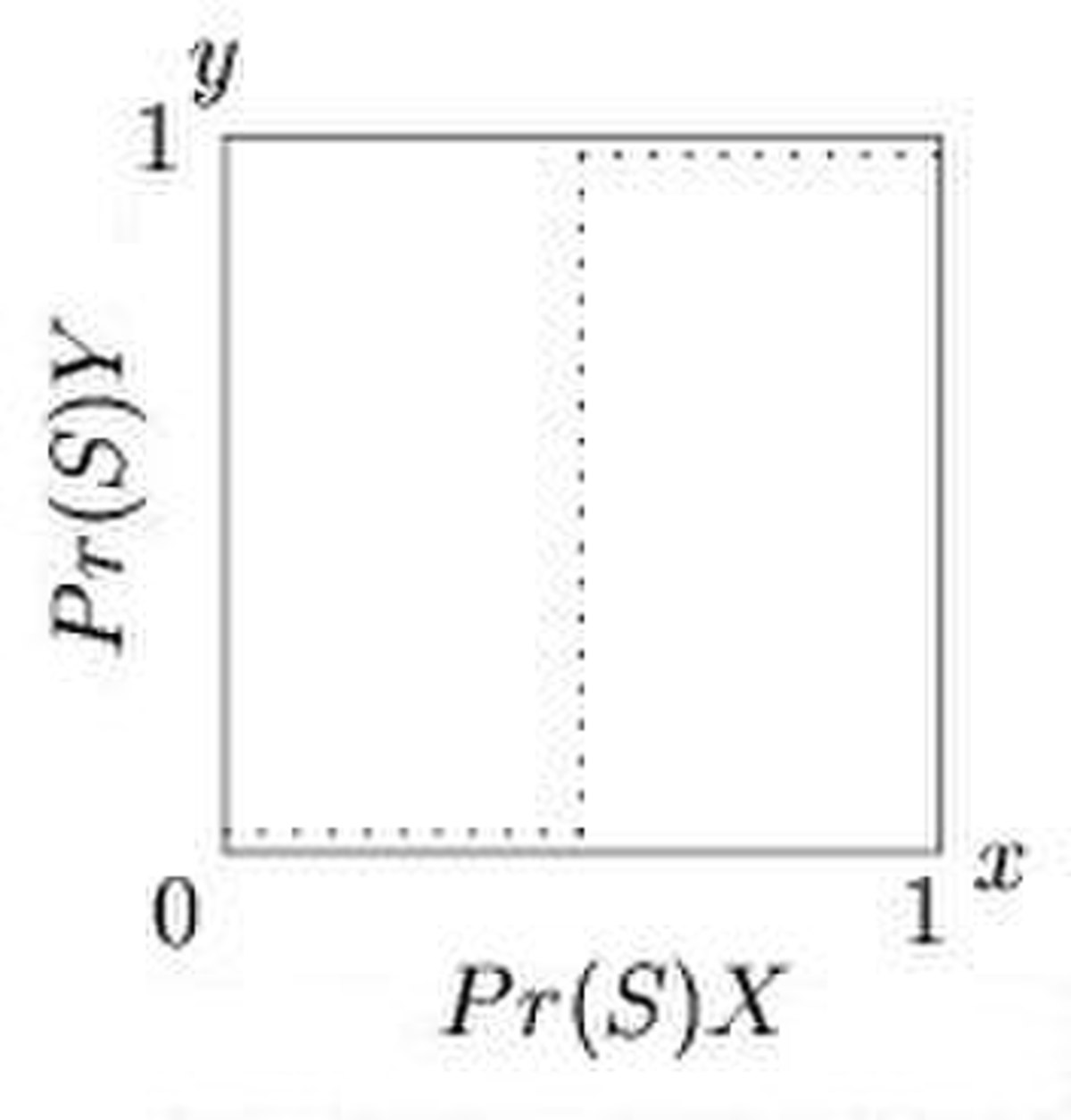
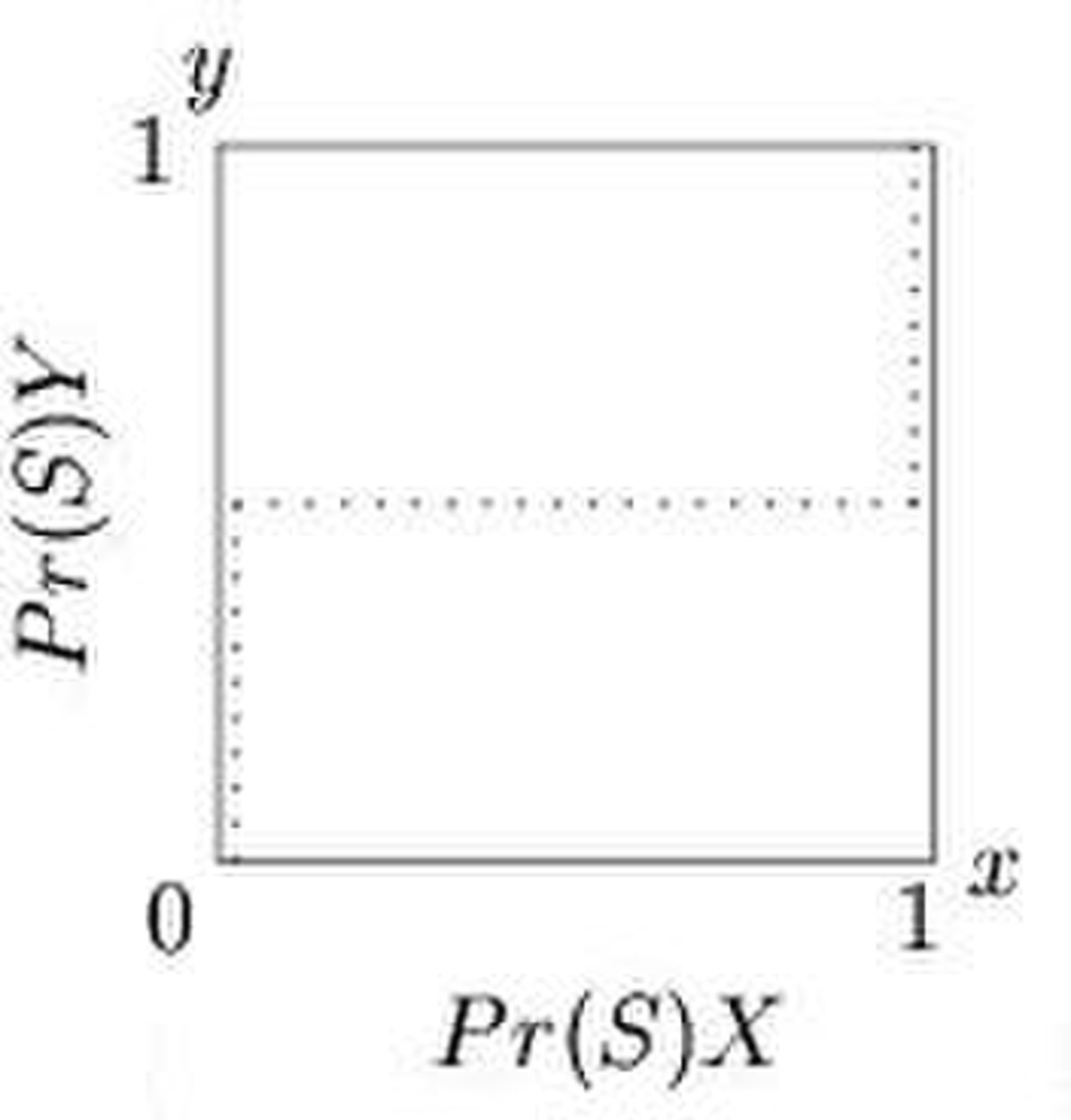
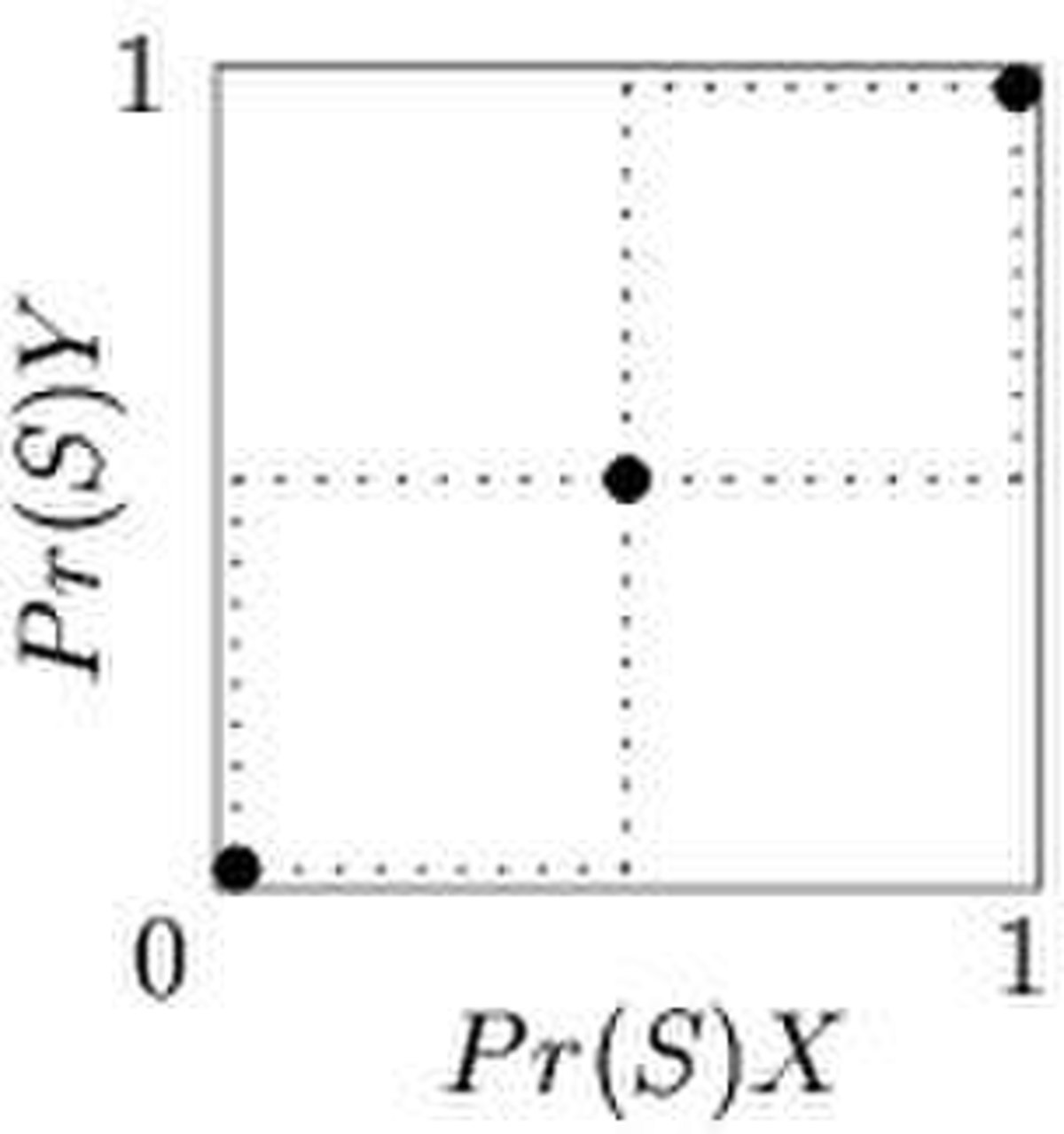
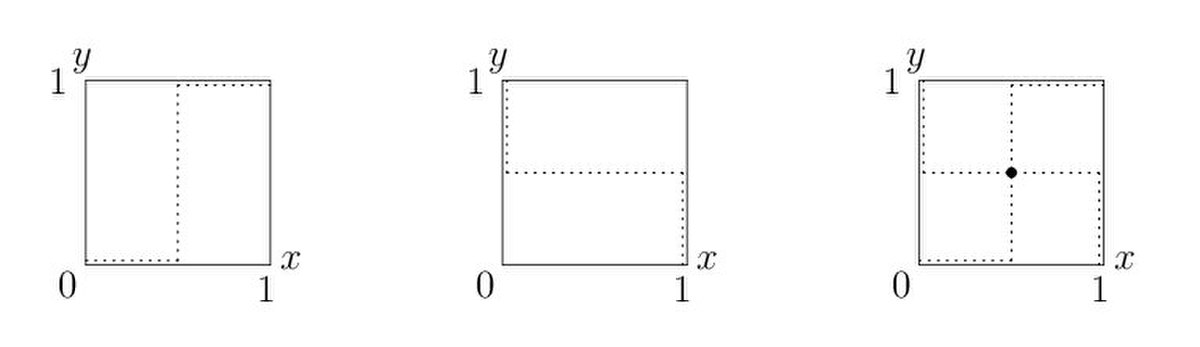
Pour tous les jeux s'exprimant sous forme normale, les fonctions de meilleure réponse peuvent être représentées par une droite dans chaque cellule. Par exemple, dans la Figure 1, la ligne pointillée dénote la probabilité optimale que le joueur Y joue « cerf » (sur l'axe y) en fonction de la probabilité que le joueur X joue « cerf » (sur l'axe x). Dans la Figure 2, la ligne pointillée dénote la probabilité optimale pour le joueur X de jouer « cerf » (axe x) comme une fonction de la probabilité que le joueur Y joue « cerf » (axe y). Remarquez que la figure 2 inverse l'ordre habituel des axes, de manière à pouvoir superposer les figures 1 et 2 afin de déterminer l'équilibre de Nash, lieu où les fonctions de meilleure réponse s'intersectent, et donc les meilleures réponses sont compatibles (Figure 3).

Fig.3 - Fonctions de réactions pour les deux joueurs dans le jeu de la chasse au cerf. L'équilibre de Nash est noté par les points soulignant les lieux où les meilleures réponses sont compatibles.

Jeux de coordination

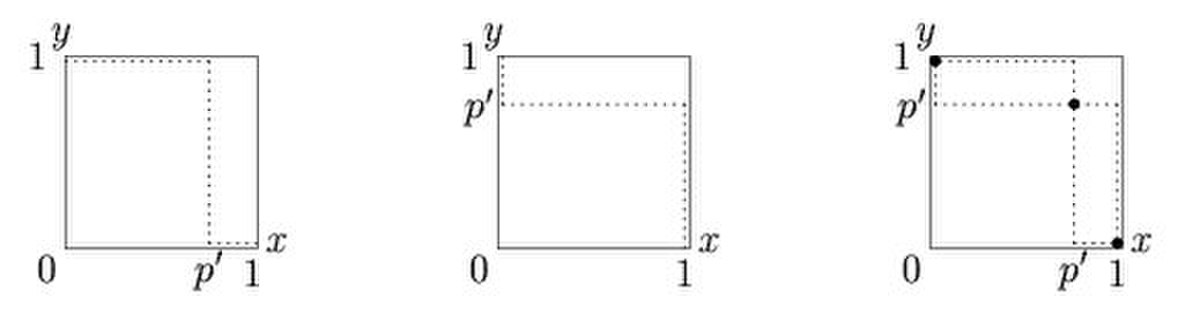
Dans les jeux où les paiements sont plus élevés quand les deux joueurs adoptent la même stratégie, comme le jeu de la Chasse au cerf ou la Guerre des sexes, les fonctions de réaction auront des formes similaires à celles de la Figure 3, avec trois équilibres de Nash, l'un dans le coin inférieur gauche, l'autre dans le coins inférieur droit et un équilibre en stratégies mixtes le long de la première diagonale, la position exacte de ce dernier équilibre dépendant des paiements du jeu.

Jeux d'anti-coordination

Dans les jeux comme le jeu de la poule ou le jeu des faucons et des colombes les paiments sont les plus élevés quand les joueurs choisissent des stratégies différentes. Leurs fonctions de réaction se croisent alors dans le sens opposé au cas des jeux de coordination. La Figure 4 illustre les fonctions de réaction pour les joueurs dans un jeu d'anti-coordination. Pour ces jeux, il existe en général trois équilibres de Nash, un dans le coin supérieur gauche, un dans le coin inférieur droit, et un sur la diagonale en stratégies mixtes. Si le joueur ignorent le type de l'autre, alors l'équilibre en stratégies mixtes est une stratégie évolutionnairement stable (SES), le jeu se déroulant sur la première diagonale. Sinon, il existe une asymétrie de non-corrélation, et les équilibres dans les coins sont également des SES.

Fig.4 - Fonctions de réaction dans le jeu des faucons et des colombes. Les équilibres de Nash correspondent au lieu d'intersection des fonctions de meilleure réponse.

Jeux avec stratégies dominées

Fig. 5 - Fonction de réaction pour un jeu avec stratégie dominée.

Dans les jeux présentant une stratégie dominée, les fonctions de meilleure réponse auront un unique point d'intersection, dans le coin inférieur gauche ou supérieur droit pour les jeux symétriques. Par exemple, dans le dilemme du prisonnier à un coup, coopérer n'est optimal pour aucune probabilité que l'autre coopère. La figure 5 illustre les fonctions de meilleure réponse pour un tel jeu. Si les axes portent la probabilité de coopérer, l'équilibre de Nash est dans le coin inférieur gauche, où aucun joueur ne coopère. S'il s'agit des probabilités de trahir, les deux courbes se coupent dans le coin supérieur droit.

Autres jeux

Les trois cas envisagés ci-dessus (coordination, anti-coordination, stratégies dominées) sont les seuls types de cas possibles pour des jeux 2x2 symétriques (à l'exception d'un quatrième cas, trivial, où les paiements sont égaux pour toutes les stratégies).

En présence d'asymétries dans les paiements, une plus grande diversité de fonctions de réactions est possible. Pour chaque joueur, il y a ainsi cinq types possibles de forme de meilleure réponse, ainsi qu'illustré par la Figure 6. De gauche à droite : stratégie dominée (toujours jouer 2), stratégie dominée (toujours jouer 1), croissante (jouer 2 si la probabilité que l'autre joueur joue 2 est supérieure à un certain seuil), décroissante (jouer 2 si la probabilité que l'autre joueur que 1 est supérieure à un certain seuil), indifférente (les deux stratégies sont équivalentes quelle que soit la stratégie de l'autre joueur).

Fig. 6 - Les cinq fonctions de meilleure réponse possibles pour un jeu 2x2. Les axes sont orientés selon la probabilité croissante qu'un joueur joue la stratégie 1. De gauche à droite : A) Toujours jouer2, la stratégie 1 est dominée; B) Toujours jouer 2, la stratégie 1 est dominée; C) La stratégie 1 est meilleure quand l'adversaire joue 1 et 2 est meilleure quand l'adversaire joue 2; D) La stratégie 1 est meilleure quand l'adversaire joue 2 et la stratégie 2 est meilleure quand l'adversaire joue 1; E) Les deux stratégies sont équivalentes quelle que soit la stratégie de l'adversaire.

Alors qu'il n'existe que quatre structures de paiement possibles pour un jeu 2x2 symétrique, l'existence de cinq types de meilleures réponses dans le cas des jeux asymétriques permet d'envisager un grand nombre de jeux différents. Toutefois, beaucoup de ceux-ci ne sont pas réellement différents l'un de l'autre, les dimensions pouvant être redéfinies (en échangeant les noms des stratégies) pour produire des jeux symétriques logiquement identiques.

Pair ou impair

Un exemple de référence de jeu avec paiements asymétriques est le jeu Pair ou impair. Dans ce jeu, le joueur Ligne (représenté sur l'axe y) gagne si les deux joueurs choisissent la même parité, alors que le joueur Colonne (représenté sur l'axe des x) gagne s'ils choisissent des parités différentes. La fonction de réaction du joueur Y est celle j'un jeu de coordination, alors que celle du joueur X correspond à un jeu d'anti-coordination. L'équilibre de Nash en stratégies mixtes est alors évolutionnairement stable.

Fig.7 - Fonctions de réaction pour le jeu Pair ou Impair. La fonction de gauche est celle d'un jeu de coordination, celle du milieu d'un jeu d'anti-coordination. L'unique équilibre de Nash est un équilibre en stratégies mixtes, illustré à droite. Il est évolutionnairement stable.