Mécanique quantique - Définition
La liste des auteurs de cet article est disponible ici.
Les inégalités de Heisenberg
Les relations d'incertitude de Heisenberg traduisent l'impossibilité de préparer un état quantique correspondant à des valeurs précises de certains couples de grandeurs conjuguées. Ceci est lié au fait que les opérateurs quantiques associés à ces grandeurs classiques ne commutent pas.
Inégalité position-impulsion
Considérons par exemple la position

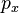
La relation d'incertitude est définie à partir des écarts quadratiques moyens de grandeurs conjuguées. Dans le cas de la position

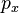
Plus l'état possède une distribution resserrée sur la position, plus sa distribution sur les valeurs de l'impulsion qui lui est associée est large. Cette propriété rappelle le cas des ondes, via un résultat de la transformée de Fourier, et exprime ici la dualité onde-corpuscule. Il est clair que ceci mène à une remise en cause de la notion classique de trajectoire comme chemin continu différentiable.
Inégalité temps-énergie
Il existe également une relation d'incertitude portant sur l'énergie d'une particule et la variable temps. Ainsi, la durée
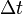

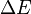
Cependant, la dérivation de cette inégalité énergie-temps est assez différente de celle des inégalités position-impulsion.
En effet, si le hamiltonien est bien le générateur des translations dans le temps en mécanique hamiltonienne, indiquant que temps et énergie sont conjuguées, il n'existe pas d'opérateur temps en mécanique quantique (« théorème » de Pauli), c'est-à-dire qu'on ne peut pas construire d'opérateur
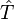
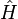
ceci pour une raison très fondamentale : la mécanique quantique a en effet été inventée pour que chaque système physique stable possède un état fondamental d'énergie mininum. L'argument de Pauli est le suivant : si l'opérateur temps existait, il posséderait un spectre continu. Or, l'opérateur temps, obéissant à la relation de commutation canonique, serait aussi le générateur des translations en énergie. Ceci entraîne alors que l'opérateur hamiltonien posséderait lui aussi un spectre continu, en contradiction avec le fait que l'énergie de tout système physique stable se doit d'être bornée inférieurement.
Mécanique quantique et relativité
La mécanique quantique est une théorie non relativiste : elle n'incorpore pas les principes de la relativité restreinte. En appliquant les règles de la quantification canonique à la relation de dispersion relativiste, on obtient l'équation de Klein-Gordon (1926). Les solutions de cette équation présentent toutefois de sérieuses difficultés d'interprétation dans le cadre d'une théorie censée décrire une seule particule : on ne peut notamment pas construire une densité de probabilité de présence partout positive, car l'équation contient une dérivée temporelle seconde. Dirac cherchera alors une autre équation relativiste du premier ordre en temps, et obtiendra l'équation de Dirac, qui décrit très bien les fermions de spin un-demi comme l'électron.
La théorie quantique des champs permet d'interpréter toutes les équations quantiques relativistes sans difficulté.
L'équation de Dirac incorpore naturellement l'invariance de Lorentz avec la mécanique quantique, ainsi que l'interaction avec le champ électromagnétique mais qui est traité encore de façon classique (on parle d'approximation semi-classique). Elle constitue la mécanique quantique relativiste. Mais du fait précisément de cette interaction entre les particules et le champ, il est alors nécessaire, afin d'obtenir une description cohérente de l'ensemble, d'appliquer la procédure de quantification également au champ électromagnétique. Le résultat de cette procédure est l'électrodynamique quantique dans laquelle l'unité entre champ et particule est encore plus transparente puisque désormais la matière elle aussi est décrite par un champ. L'électrodynamique quantique est un exemple particulier de théorie quantique des champs.
D'autres théories quantique des champs ont été développées par la suite au fur et à mesure que les autres interactions fondamentales ont été découvertes (théorie électrofaible, puis chromodynamique quantique).
![\left[ \hat{x}^i , \hat{p}_j \right] f( \vec{r} ) \ = \ \left( \hat{x}^i \hat{p}_j - \hat{p}_j \hat{x}^i \right) f( \vec{r} ) \ = \ i \hbar \ \delta^i_j \ f( \vec{r} )](https://static.techno-science.net/illustration/Definitions/autres/6/62362cb0af883942cfabebfe7554c591_b52fc05cc97a3dc589474d8123670b7f.png)
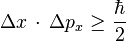
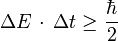
![\left[ \hat{H} , \hat{T} \right] \ = \ i \hbar \ \hat{1}](https://static.techno-science.net/illustration/Definitions/autres/3/3a765ef8f1a765c0c92401c2bf39d3f8_09a19a09cda413f4140b60be71a62c64.png)

















































