Mécanique matricielle - Définition

Introduction

La mécanique matricielle est une formulation de la mécanique quantique construite par Werner Heisenberg, Max Born, et Pascual Jordan en 1925.

La mécanique matricielle est la première définition complète et correcte de la mécanique quantique. Elle prolonge le modèle de Bohr en décrivant la manière dont se produisent les sauts quantiques, en interprétant les propriétés physiques des particules comme des matrices évoluant dans le temps. Cette description est équivalente à la formulation en termes d'ondes de Schrödinger de la mécanique quantique, et est la base de la notation bra-ket de Paul Dirac pour la fonction d'onde.

Développement

En 1925, Werner Heisenberg, Max Born, et Pascual Jordan formulèrent la description par mécanique matricielle de la mécanique quantique.

Début à Heligoland

En 1925, Werner Heisenberg travaillait, à Göttingen, sur le problème du calcul des raies spectrales de l'hydrogène. Courant mai 1925, W. Heinsenberg avait commencé à décrire les systèmes atomiques en termes d'observables exclusivement. Le 7 juin, afin d'échapper aux symptômes d'une mauvaise crise de rhinite allergique, W. Heisenberg partit pour l'île d'Heligoland en Mer du Nord, d'où le pollen est quasiment absent. Une fois là-bas, entre l'escalade et l'apprentissage par cœur des poèmes issus du Divan occidental-oriental de Goethe, il continua à réfléchir au problème spectral et réalisa sans doute que l'utilisation d'observables non-commutatives pourraient le résoudre, et il écrivit plus tard : « Il était environ trois heures du matin lorsque la solution aboutie du calcul m'apparut. Je fus tout d'abord profondément secoué. J'étais si excité que je ne pouvais songer à dormir. J'ai donc quitté la maison et attendu l'aube au sommet d'un rocher. ».

Les trois articles

Après son retour à Göttingen, Werner Heisenberg montra à Wolfgang Pauli ses calculs, commentant son point de vue : « tout est toujours vague et flou pour moi, mais il semble que les électrons ne se déplacent plus sur des orbites ». Le 9 juillet, W. Heinsenberg donna le même article à Max Born, lui indiquant : « qu'il avait écrit un article invraisemblable et qu'il n'osait pas l'envoyer pour publication, et que Born devrait le lire et lui donner son avis sur celui-ci » avant publication. Werner Heisenberg partit ensuite pour un temps, laissant Max Born analyser l'article.

Dans l'article, Werner Heisenberg formula la théorie quantique sans utiliser d'orbites électroniques fines. Hendrik Kramers avait auparavant calculé les intensités relatives des raies spectrales dans le modèle de Sommerfeld en interprétant les coefficients de Fourier des orbites comme des intensités. Mais sa réponse, comme tous les autres calculs dans l'ancienne théorie quantique, n'étaient correctes que pour des grandes orbitales.

Werner Heisenberg, après une collaboration avec Kramers, commença à comprendre que les probabilités de transition n'étaient ni des quantités quasiment classiques, parce que les seules fréquences qui apparaissent dans les séries de Fourier devraient être celles qui sont observées dans les sauts quantiques, ni les quantités fictives provenant de l'analyse de Fourier des orbites fines classiques. Il remplaça les séries de Fourier classiques par une matrice de coefficients, une sorte d'analogue quantique des séries de Fourier. En physique classique, les coefficients de Fourier donnent l'intensité de la radiation émise, donc en mécanique quantique, les valeurs des éléments de matrice sont identifiés aux intensités des raies spectrales.

Les quantités de la formulation d'Heisenberg sont la position et la quantité de mouvement classiques, mais ils n'y sont plus définis de manière précise désormais. Chaque quantité était représentée par des coefficients de Fourier à deux indices, correspondant aux états initial et final. Lorsque Max Born lut cet article, il reconnut la formulation comme étant transposable et extensible au langage systématique des matrices, qu'il avait appris lors de son étude avec Jakob Rosanes à l'université de Wrocław. Max Born, aidé de son assistant et ancien étudiant Pascual Jordan, commença immédiatement la transposition et l'extension, et ils soumirent leurs résultats à publication ; l'article fut admis à la publication tout juste 60 jours après celui d'Heisenberg. Un article continuant ce travail fut soumis à publication avant la fin de l'année par les trois auteurs ensemble (un bref aperçu du rôle de Max Born dans le développement de la formulation matricielle de la mécanique quantique avec une discussion de la formule-clé impliquant la non-commutativité des amplitudes de probabilité peut être vu dans un article de Jeremy Bernstein). Un compte-rendu détaillé historique et technique peut être consulté dans le livre de Mehra et Rechenberg The Historical Development of Quantum Theory. Volume 3. The Formulation of Matrix Mechanics and Its Modifications 1925–1926..

Jusqu'à ce moment, les matrices étaient rarement utilisées par les physiciens, étant considérées comme appartenant aux mathématiques pures. Gustav Mie les avait utilisé dans un article sur l'électrodynamique en 1912 et Max Born les avait employé dans son travail sur la théorie des réseaux cristallins en 1921. Alors que les matrices étaient utilisées pour ces domaines, l'algèbre matricielle avec ses multiplications ne correspondait pas à la description qu'ils avaient fait dans la formulation matricielle dans la mécanique quantique. Born, cependant, avait appris l'algèbre matricielle avec Rosanes, comme indiqué précédemment, mais avait aussi appris la théorie de Hilbert sur les équations intégrales et formes quadratiques pour un nombre infini de variables comme il en ressort d'une citation de Born sur le travail de Hilbert Grundzüge einter allgemeinen Theroire der Linearen Integralgleichungen publié en 1912. Jordan était également apte pour cette tâche. Pendant un certain nombre d'années, il a été l'assistant de Richard Courant à Göttingen pour la préparation du livre de Courant et Hilbert Methoden der mathematischen Physik I, publié en 1924. Ce livre, de manière fortuite, contenait une grande partie des outils mathématiques nécessaires pour le développement continu de la mécanique quantique.

Le raisonnement d'Heisenberg

Avant l'énoncé de la mécanique matricielle, la théorie quantique décrivait le mouvement d'une particule par une orbite classique X(t),P(t) avec la restriction que l'intégrale temporelle sur une période T de la quantité de mouvement par la vitesse doit être un multiple entier positif de la constante de Planck :

Alors que cette restriction sélectionne correctement les orbites avec plus ou moins les bonnes valeurs d'énergie E_n, le formalisme de l'ancienne théorie quantique ne décrivait pas les processus dépendants du temps, comme l'émission ou l'absorption de radiation.

Quand une particule classique est faiblement couplée à un champ radiatif, l'amortissement radiatif pouvant ainsi être négligé, il émet une radiation dans un motif se répétant à chaque période d'orbitale. Les fréquences construisant l'onde émise sont donc des multiples entiers de la fréquence d'orbitale, ce qui est le reflet du fait que X(t) est périodique, la représentation de Fourier n'ayant donc que des fréquences 2πn / T exclusivement.

Les coefficients X_n sont des nombres complexes. Ceux à fréquences négatives doivent être les complexes conjugués de ceux à fréquences positives, de telle façon à ce que X(t) soit toujours réel,

.

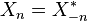Une particule mécanique quantique, d'un autre côté, ne peut émettre de radiation continument, et peut seulement émettre des photons. Si l'on suppose que la particule quantique initialement dans l'orbite n, émettant un photon, puis aboutissant dans l'orbite m, l'énergie du photon est E_n − E_m, ce qui signifie que sa fréquence est (E_n − E_m) / h.

Pour de grands n et m, mais avec une différence n-m relativement faible, le principe de correspondance de Bohr :

.

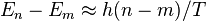Dans la formule ci-dessous, T est la période classique soit de l'orbite classique n ou de l'orbite m, la différence entre elles étant d'ordre plus élevé en h. Mais pour de petits n et m, ou si n − m est important, les fréquences ne sont plus des multiples entiers d'une simple fréquence.

Les fréquences émises par la particule étant les mêmes que les fréquences dans la description de Fourier de son mouvement, cela suggère que quelque chose dans la description en dépendance temporelle de la particule oscille avec la fréquence (E_n − E_m) / h. Werner Heisenberg a appelé cette quantité X_nm, et postula qu'il pourrait être réduit aux coefficients de Fourier dans les limites classiques. Pour des valeurs importantes de n et m, mais avec n-m relativement faible, X_nm est le (n-m)^e coefficient de Fourier du mouvement classique à l'orbite n. X_nm étant de fréquence opposée à X_mn, la condition pour que X soit réelle devient :

.

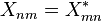Par définition, X_nm seul possède la fréquence (E_n − E_m) / h, donc son évolution temporelle est simple :

.

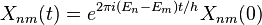C'est la forme originale de l'équation du mouvement d'Heisenberg.

Étant données deux matrices X_nm et P_nm décrivant deux quantités physiques, Heisenberg pouvait alors construire une nouvelle matrice du même type en combinant les termes X_nkP_km, oscillant aussi avec la fréquence adéquate. Les coefficients de Fourier du produit des deux quantités étant la convolution des coefficients de Fourier pris chacun séparément, la correspondance avec les séries de Fourier permit à Heisenberg de déduire la règle de multiplication des matrices :

.

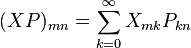Born souligna que c'est la règle de multiplication de l'algèbre matricielle, ce qui signifie que la position, le moment, l'énergie et toutes les quantités observables dans la théorie peuvent être interprétées en termes de matrices. En raison de la règle de multiplication, le produit dépend de son ordre : XP peut être différent de PX (non-commutativité).

La matrice X est une description complète du mouvement d'une particule quantique. Les fréquences du mouvement quantique n'étant pas des multiples d'une fréquence commune, les éléments de matrice ne peuvent être interprétés en termes de coefficients de Fourier d'une trajectoire classique clairement définie. Néanmoins, comme matrices, X(t) et P(t) satisfont aux équations classiques du mouvement.