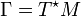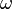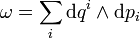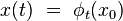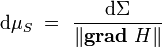Mécanique hamiltonienne - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Équations canoniques de Hamilton - Flot hamiltonien - Espace des phases

Flot hamiltonien

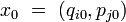
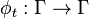
L'évolution dynamique du système selon les équations canoniques de Hamilton à partir d'une condition initiale $x_0 \ = \ (q_{i0},p_{j0})$ engendre le flot hamiltonien $\phi_t : \Gamma \to \Gamma$ , c’est-à-dire le groupe continu à un paramètre tel que :

La succession des positions $x (t)$ dans l'espace des phases se traduit par une courbe continue, appelée orbite.

Théorème de Liouville

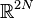
Le flot hamiltonien préserve la mesure de Liouville sur l'espace des phases. Lorsque celui-ci est euclidien, cette mesure invariante sous le flot est simplement la mesure de Lebesgue sur $\mathbb{R}^{2N}$ :

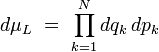
La démonstration de ce théorème repose sur le fait que la divergence de la « vitesse » dans l'espace des phases est nulle :

où on a utilisé les équations canoniques pour conclure. Autrement dit, le « fluide hamiltonien » dans l'espace des phases est incompressible.

Hypersurface d'énergie constante

Un système hamiltonien invariant par translation dans le temps satisfait toujours à la conservation de l'énergie :

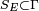
de telle sorte que sa dynamique est en fait toujours restreinte à une hypersurface $\scriptstyle S_E \subset \Gamma$ à $2 N - 1$ dimensions. Dans ce cas, la mesure de Liouville invariante sous le flot dans l'espace des phases induit une mesure invariante sous le flot sur l'hypersurface d'énergie constante, définie par :

où $dΣ$ est la mesure sur l'hypersurface S induite par la métrique sur l'espace des phases.

Système intégrable

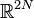
Il peut exister d'autres constantes du mouvement indépendantes de l'énergie en plus de celle-ci. Lorsqu'un système invariant par translation défini sur ${\mathbb R}^{2N}$ dans le temps possède N constantes du mouvement indépendantes, on dit qu'il est intégrable. Sa dynamique est alors particulièrement simple.

Espace des phases

Dynamique dans l'espace euclidien

Considérons un système à $N$ degrés de liberté décrits à l'instant $t$ par :

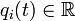
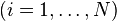
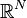
les $N$ coordonnées généralisées $q_i(t) \in \mathbb{R}$ , $(i = 1, \dots, N)$ . On peut voir ces coordonnées comme les composantes d'un vecteur de $\mathbb{R}^N$ .

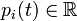
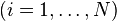
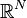
les $N$ moments conjugués $p_i(t)\in \mathbb{R}$ , $(i = 1, \dots, N)$ . On peut également voir ces coordonnées comme les composantes d'un autre vecteur de $\mathbb{R}^N$ .

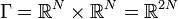
À chaque instant, les $2 N$ coordonnées $(q i (t), p i (t))$ définissent un point $x (t)$ dans l'espace des phases $\Gamma = \mathbb{R}^N \times \mathbb{R}^N = \mathbb{R}^{2N}$ à 2N dimensions.

Dynamique sur une variété différentiable

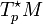
Considérons un système à $N$ degrés de liberté dont les $N$ coordonnées généralisées $q i (t)$ précisent la position d'un point $p$ sur une variété différentielle $M$ à N dimensions.. Le moment conjugué $p j (t)$ est alors un élément de l'espace cotangent $T_p^{\star}M$ dans la direction j.

A chaque instant, les $2 N$ coordonnées $(q i (t), p j (t))$ définissent dans ce cas un point $x (t)$ dans l'espace des phases $\Gamma = T^{\star}M$ qui s'identifie à l'espace fibré cotangent à 2N dimensions. Cet espace des phases est naturellement muni de la forme symplectique $\omega\,$ définie par