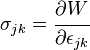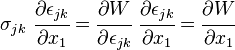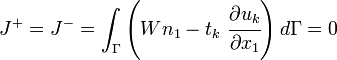Mécanique de la rupture - Définition
La liste des auteurs de cet article est disponible ici.
Intégrale J
L'intégrale-J (intégrale curviligne) représente un moyen de calculer le taux de relaxation de l'énergie de déformation ou de travail (énergie) par unité de surface de zone rompue au sein d'un matériau. Le concept théorique de l'integral-J a été développé, de façon indépendante, en 1967 par Cherepanov et en 1968 par Jim Rice. Ces travaux mettent en évidence que le contour délimitant la zone plastique aux abords du front de fissure (appelé J) est indépendant du profile (contour) de la fissure.
Par la suite, des méthodes expérimentales ont été élaborées pour permettre la mesure des propriétés de rupture de critiques à partir d'échantillons à l'échelle du laboratoire pour des matériaux dans lesquels la dimensions des prélèvements est insuffisante pour garantir la validité les hypothèses de la mécanique linéaire élastique de la rupture, et d'en déduire une valeur critique de l'énergie de rupture J1c.
La quantité J1c définit le point à partir duquel se forme une zone plastique dans le matériau au moment de la propagation et pour un mode de chargement.
L'intégrale-J est équivalente au taux de relaxation de l'énergie de déformation d'une fissure dans un solide soumis à une charge constante. Cela est vrai, dans des conditions quasi-statiques, tant pour les matériaux linéairement élastiques que pour les échantillons expérimentés à petite échelle en passe de céder en front de fissure.
Critère d'énergie
Lorsque la variation d'énergie élastique est supérieure à la variation d'énérgie superficielle il y a propagation de la fissure ce qui correspond à une diminution de l'énergie libre du système. Dans une plaque de dimension infinie en matériau idéalement élastique contenant une fissure, celle-ci se propage lorsque :
Avec
- E = Module de Young, et
- σr = contrainte de rupture.
2Eγs correspond à l'énergie nécessaire pour créer une surface unité de fissuration. Il s'agit en fait d'une énergie critique que l'on note : G1c en J.m − 2.
On peut donc réécrire (12) comme suit :
Les deux critères K1c et G1c caractérise la propagation brutale d'une fissure. Ces deux critères sont liés par les relations :
Pour un état de déformations planes, cas des structures épaisses ;
avec
- ν = module de Poisson.
Pour un état de contraintes planes, cas des structures minces ;
Integrale-J et rupture ductile
Pour les matériaux isotropes présentant une transition ductile / fragile marquée , l'intégrale-J peut être directement liée au mode de rupture ductile.
Dans le cas d'une déformation plane dans les conditions de chargement correpondant au mode I, la relation est donnée par :
Avec :
- GIc le facteur de relaxation de l'énergie de déformation critique,
- KIc le facteur d'intensité de contrainte en rupture ductile sous chargement en mode I,
- ν le coéficient de Poisson, et
- E le module de Young du matériau.
Dans le cas d'un chargement en mode II, la relation entre l'intégrale-J et la rupture ductile en mode II, (KIIc) est donné par :
Dans le cas d'un chargement en mode III, la relation est donnée par :
Integrale-J a deux dimensions
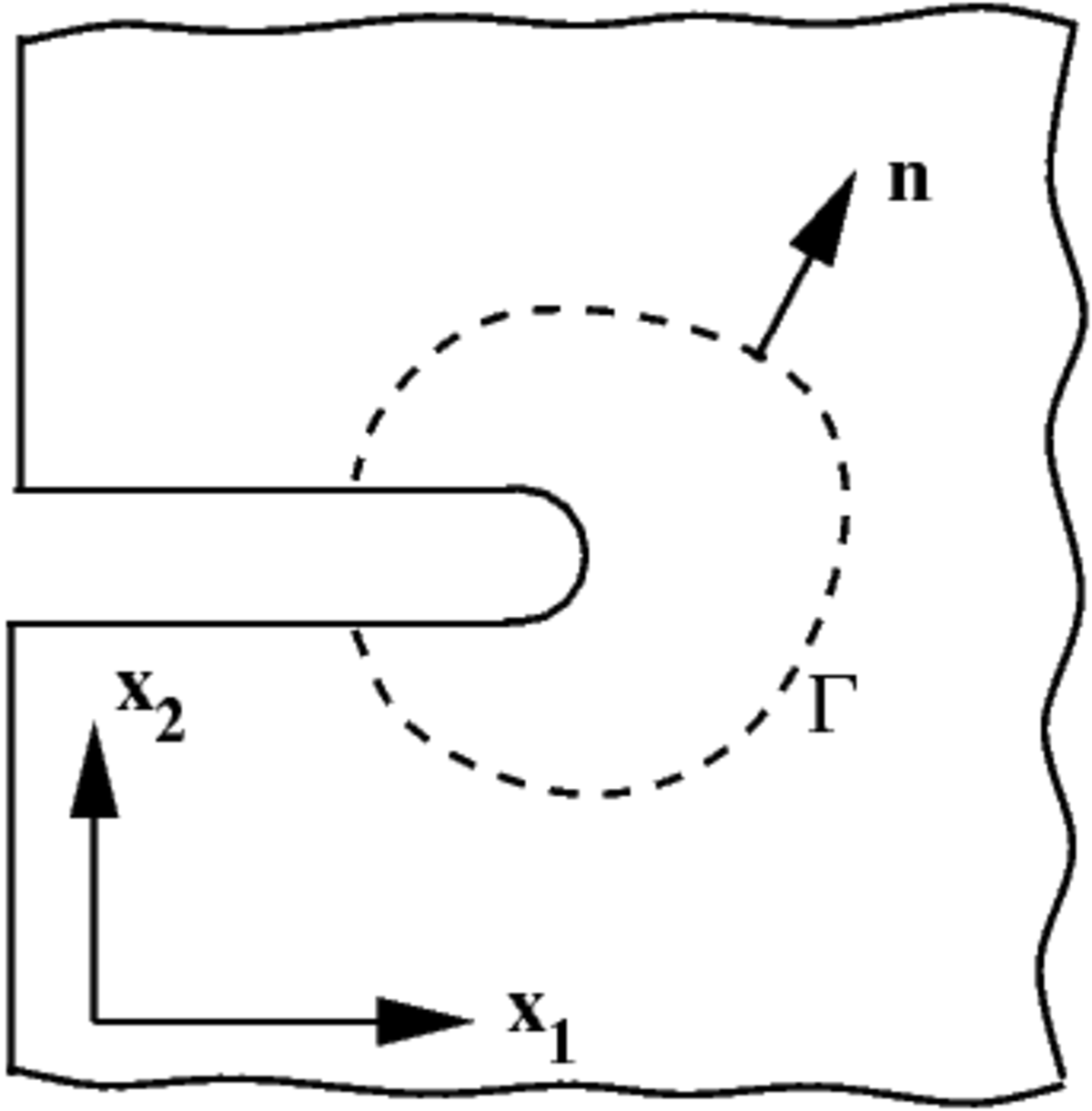
L'intégrale-J à deux dimensions a été définie à l'origine par (voir figure ci contre)
Avec :
- W(x1,x2) est la densité d'énergie de déformation,
- x1,x2 sont les deux directions,
-
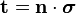
-
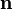
- Γ, σ est le tenseur de contrainte de Cauchy, et
-
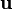
L'énergie de déformation est donnée par :
L'intégrale-J aux abords d'un front de fissure est fréquemment exprimée, sous sa forme générale (et en notation d'Einstein), par :
Avec :
- Ji est la composante de l'intégrale-J pour une ouverture de fissure dans la direction xi,
- ε est une petite région aux abord du front de fissure.
En utilisant le théorème de Green nous pouvons montrer que cette intégrale prend la valeur zéro quand la courbe Γ est fermé, que la région ainsi délimitée ne contient pas de point singulier et forme une surface de genre 0. Si les faces de la fissure ne sont pas sous tension, alors l'intégrale-J est indépendante.
Rice a également démontré que la valeur de l'intégrale-J représente le taux de relaxation d'énergie pour la propagation des fissures planes.
L'intégrale-J a été développée pour résoudre des difficultés rencontrées dans le calcul des contraintes aux abords d'une fissure dans un matériau linéairement élastique. Rice a montré qu'en mode de chargement constant et sans atteindre l'adaptation plastique, l'intégrale-J peut aussi être utilisée pour calculer le taux de relaxation d'énergie dans un matériau plastique.
-
Démonstration de la valeur zéro de l'intégrale-J sur une courbe fermé Pour montrer l'indépendance de l'intégrale-J, nous devons d'abord montrer qu'elle prend la valeur zéro sur une courbe fermée délimitant une région de genre 0. Prenons simplement l'expression J1 donnée par : Nous pouvons écrire que :
D'après le théorème de Green nous avons :
En utilisant ce résultat nous pouvons exprimer J1 comme :
Avec :
- A l'aire contenue dans le chemin Γ.
Maintenant, si il n'y aucune force présente, l'état d'équilibre (conservation du moment linéaire) impose que :
Aussi :
Donc :A partir de l'équilibre du moment angulaire nous avons σjk = σkj. Par conséquent :
L'intégrale-J peut s'écrire :
Maintenant, pour un matériau élastique la contrainte peut être dérivée de la fonction de l'énergie de stockée W en utilisant :
Donc, en différenciant :
C'est pourquoi nous obtenons J1 = 0 pour une courbe fermée de genre 0 une région sans point singulier (poit où la contrainte serait infinie).
-
-
Démonstration de l'indépendance de la courbe définit pat l'intégrale-J Fichier:J integralPathIndep.pngfigure 4. Courbe aux abord d'une entaille en deux dimensions.Considerons le contourr Γ = Γ1 + Γ + + Γ2 + Γ − . Dans la mesure où cette courbe est fermée et délimite une région de genre 0, l'intégrale-J sur cette courbe prend la valeur zéro (cf paragraphe ci dessus).
- J = J(1) + J + − J(2) − J − = 0
On admet que les intégrales antihoraires autour de la pointe de la fissure sont de signe positif. Or, puisque les faces de la fissure sont parallèles à l' axe x2, la composante normale à ces faces n1 = 0. Aussi, tant que ces surface ne sont pas sous tension ; tk = 0 et il vient :
Donc,
- J(1) = J(2)
et l'intégrale-J est une courbe indépendante.
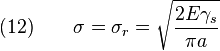
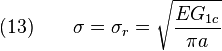
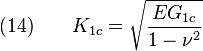
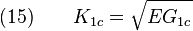
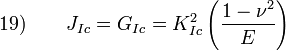
![20) \qquad J_{IIc} = G_{IIc} = K_{IIc}^2 \left[\frac{4(1-\nu^2)}{3E}\right]](https://static.techno-science.net/illustration/Definitions/autres/c/c44a6df90f8d98ff88362c0a6d157792_fa4e0e84c6285bf4366b794403e2a32f.png)
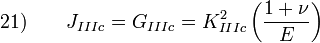
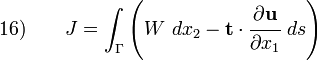
![17) \qquad W =\int_0^\epsilon \boldsymbol{\sigma}:d\boldsymbol{\epsilon} ~;~~ \boldsymbol{\epsilon} = \tfrac{1}{2}\left[\boldsymbol{\nabla}\mathbf{u}+(\boldsymbol{\nabla}\mathbf{u})^T\right] ~.](https://static.techno-science.net/illustration/Definitions/autres/0/084f172452c063e244eb42000fe06482_df879b82c6c2e36717b46e86f5b4a3e9.png)
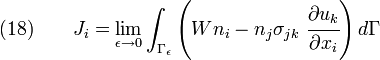
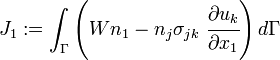
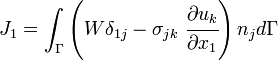
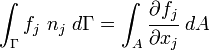
![\begin{align} J_1 & = \int_{A} \cfrac{\partial}{\partial x_j}\left(W \delta_{1j} - \sigma_{jk}~\cfrac{\partial u_k}{\partial x_1}\right) dA \\ & = \int_A \left[\cfrac{\partial W}{\partial x_1} - \cfrac{\partial\sigma_{jk}}{\partial x_j}~\cfrac{\partial u_k}{\partial x_1} - \sigma_{jk}~\cfrac{\partial^2 u_k}{\partial x_1 \partial x_j}\right]~dA \end{align}](https://static.techno-science.net/illustration/Definitions/autres/8/8fd53a298c780eb6d70753c2cd9d9b7c_171d18c6a6d4a381359d90a8bc184711.png)
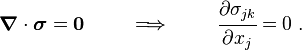
![\boldsymbol{\epsilon} = \tfrac{1}{2}\left[\boldsymbol{\nabla}\mathbf{u}+(\boldsymbol{\nabla}\mathbf{u})^T\right] \qquad \implies \qquad \epsilon_{jk} = \tfrac{1}{2}\left(\cfrac{\partial u_k}{\partial x_j} + \cfrac{\partial u_j}{\partial x_k}\right) ~.](https://static.techno-science.net/illustration/Definitions/autres/9/9fa7565bac865f3631875a6f618fecbe_36ff4e3fdf6fb59e0fc98022d2df23c6.png)
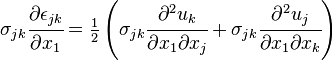
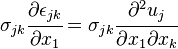
![J_1 = \int_A \left[\cfrac{\partial W}{\partial x_1} - \sigma_{jk}~\cfrac{\partial\epsilon_{jk}}{\partial x_1}\right]~dA](https://static.techno-science.net/illustration/Definitions/autres/2/2238db88f38f08ac9129731f880dc12f_986949b0f0b51b8e33198098038d25ee.png)