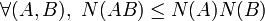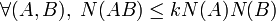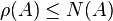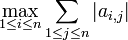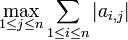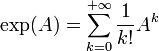Matrice (mathématiques) - Définition

Normes et rayon spectral

Dans tout ce paragraphe, les matrices considérées sont dans ou . De plus on identifie une matrice A avec l'endomorphisme de ou qui à la matrice colonne X associe la matrice colonne AX. Le cas réel et le cas complexe sont identiques.

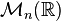
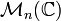
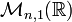
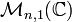
Normes et normes d'algèbre

Soit N une norme sur ou .

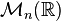
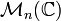
On dira que N est une norme d'algèbre (on dit aussi norme de Banach ou norme multiplicative) si et seulement si

Certains auteurs imposent en outre que N(I_n) = 1

Pour une norme quelconque, l'application bilinéaire étant continue (on est en dimension finie), on est assuré de l'existence d'une constante k > 0 telle que

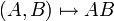
Par suite, la norme est une norme d'algèbre. Toute norme est donc proportionnelle à une norme d'algèbre.

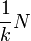
Rayon spectral

Soit A une matrice carrée à coefficients complexes. On appelle rayon spectral le plus grand module des valeurs propres de A. Dans tout ce qui suit, on notera ρ(A) le rayon spectral de A.

Théorème : Pour toute norme d'algèbre N sur (respectivement dans ) et pour toute matrice A dans (respectivement dans ), l'inégalité suivante est vérifiée :

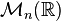
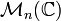
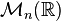
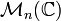
Démonstration : Soit λ une valeur propre de A et X un vecteur propre associé. notons B la matrice carrée dont la première colonne est X et les autres sont nulles. On a AB = λB donc et on peut simplifier par N(B) car le vecteur X étant non nul, il en est de même de la matrice B.

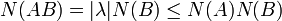
De plus, on montre que , la borne inférieure étant prise sur l'ensemble des normes subordonnées, donc a fortiori sur l'ensemble des normes d'algèbre.

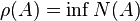
Par contre, l'égalité peut s'avérer impossible. Il suffit pour cela de considérer une matrice non nulle dont le rayon spectral est nul :

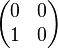
Normes subordonnées

Lorsqu'on munit d'une norme , on munit automatiquement d'une norme, appelée norme subordonnée à . Elle est donnée par la formule suivante donnée pour une matrice A quelconque dans  :

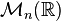
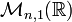
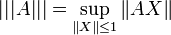
En notant , on a

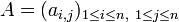
• Si , (norme infinie), alors la norme de A vaut :

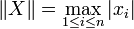
• Si , (norme indice 1), alors la norme de A vaut :

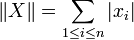
Toute norme subordonnée est une norme d'algèbre avec en plus | | | I_n | | | = 1.

La réciproque, même avec cette clause supplémentaire | | | I_n | | | = 1, est fausse. En effet, si N est subordonnée à , avec , il est nécessaire que, pour tout X, on ait . C'est une conséquence immédiate du théorème de Hahn-Banach.

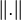
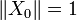
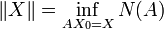
À présent, si, pour , on pose N(M) = Max( | a | + | c | ,2 | b | + | d | ), et , on vérifie toutes les propriétés attendues de N, mais le procédé précédent donne comme norme la norme classique, à laquelle N n'est pas subordonnée.

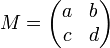
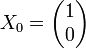
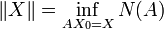
Norme subordonnée à la norme euclidienne

On se place dans la cas où est muni de sa norme euclidienne canonique donnée par .

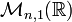
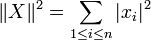
Lorsque A est une matrice symétrique (respectivement hermitienne), la norme de A est égale au rayon spectral de A.

Dans le cas où A est une matrice quelconque, la norme de A est égal à

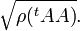
La norme de A est donc la plus grande des valeurs singulière de A (les valeurs singulière de A sont, par définition, les racines carrées des valeurs propres de ^tAA).

Exponentielle d'une matrice

Soit , Soit N une norme d'algèbre et une série entière de rayon de convergence R.

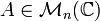
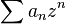
Alors si N(A) < R, la série est absolument convergente. La ruse, c'est que .

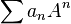
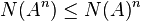
En particulier, on peut définir, pour toute matrice carrée complexe, la quantité

Le calcul effectif de cette exponentielle se fait par réduction de la matrice.

L'exponentielle joue un rôle central dans l'étude des systèmes linéaires d'équations différentielles.