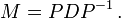Matrice diagonalisable - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
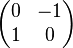
En mathématiques, une matrice diagonalisable est une matrice carrée semblable à une matrice diagonale. Cette propriété est équivalente à l'existence d'une base de vecteurs propres, ce qui permet de définir de manière analogue un endomorphisme diagonalisable d'un espace vectoriel.
Le fait qu'une matrice soit diagonalisable dépend du corps dans lequel sont cherchées les valeurs propres, ce que confirme la caractérisation par le fait que le polynôme minimal soit scindé à racines simples.
Cette caractérisation permet notamment de montrer que les projecteurs sont toujours diagonalisables, ainsi que les involutions si le corps des coefficients est de caractéristique différente de 2. Plus généralement, les endomorphismes et matrices d'ordre fini sont diagonalisables sur le corps des complexes. Au contraire, un endomorphisme nilpotent non nul ne peut pas être diagonalisable.
Les matrices réelles symétriques sont diagonalisables par une matrice orthogonale. Plus généralement les matrices normales, parmi lesquelles les matrices hermitiennes, antihermitiennes et unitaires sont diagonalisables à l'aide d'une matrice unitaire, ce qui conduit au théorème spectral.
La diagonalisation est la détermination effective d'une matrice de passage transformant une matrice diagonalisable en une matrice diagonale, ou la décomposition d'un espace vectoriel en une somme directe de droites stables par un endomorphisme.
Définitions
Approche matricielle
Une matrice carrée M à coefficients dans un corps k est dite diagonalisable sur k s'il existe une matrice inversible P et une matrice diagonale D à coefficients dans k satisfaisant la relation :
Dans ce cas, chaque vecteur colonne Y de la matrice P est un vecteur propre pour la matrice M, c'est-à-dire qu'il existe un scalaire λ sur la diagonale de D tel que MY = λY.
Réciproquement, si une matrice admet une famille de vecteurs propres qui forment une base de l'espace des vecteurs colonnes alors cette matrice est diagonalisable. Il suffit de construire la matrice inversible formée par une juxtaposition de ces vecteurs, la matrice diagonale étant définie par la suite des valeurs propres associées.
Endomorphisme
Un endomorphisme d'un espace vectoriel est dit diagonalisable s'il existe une base de vecteurs propres. Cela signifie que l'espace vectoriel peut être décomposé en une somme directe de droites stables par l'endomorphisme, ou autrement dit que l'espace vectoriel est la somme directe des sous-espaces propres de l'endomorphisme.
En dimension finie, cette définition signifie que l'endomorphisme est représenté par une matrice diagonale dans cette base, donc que n'importe quelle représentation matricielle de l'endomorphisme est une matrice diagonalisable par changement de base.
Dans une base orthonormale
Matrices symétriques
Toute matrice réelle symétrique est diagonalisable par une matrice orthogonale, c'est-à-dire que l'endomorphisme associé dans l'espace euclidien de dimension n est diagonalisable dans une base orthonormale. Réciproquement, si U est une matrice orthogonale et D une matrice diagonale réelle, alors le produit de matrices réelles UDU − 1 est une matrice symétrique.
Lorsqu'une matrice symétrique A est positive, c'est-à-dire si ses valeurs propres sont toutes positives, il existe une unique matrice symétrique positive dont le carré soit A. Cette racine carrée de A est en effet diagonalisable et a nécessairement les mêmes espaces propres avec des valeurs propres en racine carrée de celles de A.
Matrices normales
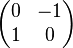
De même, toute matrice complexe hermitienne est diagonalisable par une matrice unitaire en une matrice diagonale réelle. Plus généralement, les matrices complexes diagonalisables par une matrice unitaire sont les matrices normales, c'est-à-dire qui commutent avec leur adjointe. Cette définition comprend à la fois les matrices hermitiennes, les antihermitiennes, les unitaires et en particulier leurs versions réelles : symétriques, antisymétriques et orthogonales. Cependant, ces deux dernières familles de matrice n'admettent pas en général de diagonalisation sur le corps des réels.
Application au théorème spectral
Le théorème spectral stipule qu'étant données deux formes bilinéaires symétriques sur un espace vectoriel réel ou complexe de dimension finie, si l'une d'entre elle est définie positive, il existe une base orthonormale pour celle-ci qui soit orthogonale pour l'autre.
Autrement dit, il existe une base dans laquelle les deux formes soient représentées par des matrices diagonales, la première étant même la matrice identité I. Si les deux formes ont respectivement pour matrice A et B dans une base arbitraire, et pour matrices I et B' dans la base particulière fournie par le théorème, les nouvelles matrices ne sont pas semblables aux anciennes, mais congruentes, via la matrice de passage P (inversible) et sa matrice adjointe P* :
-
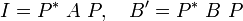
Pour démontrer le théorème il suffit de considérer, sur l'espace euclidien ou hermitien défini par la première forme, l'endomorphisme autoadjoint canoniquement associé à la seconde : il existe une base orthonormée (par rapport à la première forme) qui est propre pour cet endomorphisme (donc qui est orthogonale pour la seconde forme).