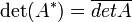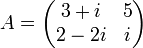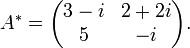Matrice adjointe - Définition

Introduction

En algèbre linéaire, une matrice adjointe (aussi appelée matrice transconjuguée) d’une matrice M à coefficients complexes est la matrice transposée de la matrice conjuguée de M. Dans le cas particulier où M est à coefficients réels, sa matrice adjointe est donc simplement sa matrice transposée.

La matrice adjointe est traditionnellement notée mais il arrive couramment de rencontrer d’autres notations :

• ou sont communément utilisés en algèbre linéaire, la seconde notation étant aussi appelée conjuguée hermitienne et plus fréquente dans le cas d’algèbres sur des espaces linéaires de fonctions ou de distributions (de dimension finie ou non).
• est la notation utilisée universellement en mécanique quantique, le plus souvent sur des algèbres de dimensions infinies, et souvent en association avec la notation bra et ket symbolisant les vecteurs d’états et matrices de transformation et simplifiant l’écriture et l’interprétation des expressions .
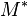
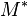
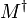
• La notation est parfois utilisée aussi, bien que ce symbole soit plutôt utilisé communément pour désigner le pseudo-inverse de Moore-Penrose.

On a donc : .

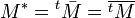
Propriétés

• 
• 
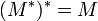
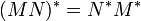
• Si A est une matrice carrée alors

Exemple

Si :

alors :