Mathématiques - Définition

Pratique mathématique

Activité de recherche

La recherche mathématique ne se limite pas qu'à la démonstration des théorèmes. L'une des méthodes les plus fructueuses de recherche mathématique est la mise en rapprochement de domaines a priori éloignés en mettant en lumière des phénomènes analogues (par exemple, la géométrie euclidienne et les équations différentielles linéaires). Voir des phénomènes analogues se produire peut conduire à vouloir adapter des résultats d'un domaine des mathématiques à un autre, à reformuler des éléments de démonstration en termes équivalents, à tenter une axiomatisation d'un objet (par exemple, ce pourrait être la notion d'espace vectoriel) qui regrouperait les deux domaines... Dans ce dernier cas, ce nouvel objet deviendrait alors un objet d'étude par lui-même. Dans certains cas, l'identification d'objets a priori différents devient nécessaire : le langage des catégories permet de faire ce genre de choses.

Une autre méthode de recherche est la confrontation aux exemples et aux cas particuliers. Cette confrontation peut permettre de réfuter des propriétés qu'on pensait ou espérait être vraies (conjectures). Au contraire, elle peut permettre de vérifier des propriétés ou d'amener à les formaliser. Par exemple, en géométrie riemannienne, l'étude des surfaces (donc des objets en dimension 2) et de leurs géodésiques a finalement conduit Anosov à formaliser le difféomorphisme d'Anosov, une transformation possédant d'intéressantes propriétés dynamiques.

Langage mathématique

Les mathématiques utilisent un langage qui leur est propre. Certains termes du langage courant, comme groupe, anneau, corps ou variété peuvent être empruntés et redéfinis pour désigner des objets mathématiques. Mais souvent des termes sont formés et introduits selon les besoins : isomorphisme, topologie, itération... Le nombre élevé de ces termes rend difficile la compréhension des mathématiques par les non-mathématiciens.

Le langage mathématique s'appuie aussi sur l'usage de formules. Elles comportent des symboles, les uns en rapport avec le calcul propositionnel comme le connecteur binaire d'implication ou le connecteur unaire de négation , d'autres en rapport avec le calcul des prédicats, comme le quantificateur universel ou le quantificateur existentiel . La plupart des notations utilisées au XXI^e siècle ont été introduites après le XVII^e siècle seulement.

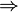
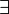
Il existe un langage mathématique qui décrit les mathématiques. En ce sens, on dit qu'il s'agit d'un métalangage : il s'agit de la logique mathématique.

Fondements

Censément, les mathématiques utilisent la logique comme outil pour démontrer des vérités organisées en théories. Une première analyse laisse espérer qu'une utilisation puissante de cet outil tellement sûr, une réduction toujours plus poussée des bases, les axiomes, sur lesquelles s'échafaude l'édifice mathématique, finissent par mener à un corpus de faits incontestables. Plusieurs obstacles se dressent pourtant.

Aristote : le fondateur de la logique formelle (peinture par Raphaël).

D'une part, en tant qu'activité humaine, les mathématiques s'éloignent du modèle d'une construction suivant scrupuleusement les lois de la logique et indépendante du réel. Citons un fait et un phénomène pour illustrer cela. Tout d'abord, les démonstrations que rédigent les mathématiciens ne sont pas formalisées au point de suivre en détail les lois de la logique, car cela est impossible en un temps raisonnablement court. Comme pour n'importe quelle science. l'acceptation de la véracité d'une démonstration, et donc d'un théorème, repose in fine sur un consensus de spécialistes au sujet de la validité de l'approximation de démonstration formelle proposée (La structure des révolutions scientifiques de Thomas Kuhn). L'avènement de l'informatique a cependant changé la donne, au moins marginalement, puisque celle-ci permet de formaliser et de vérifier des démonstrations de plus en plus complexes.

Cependant l'activité mathématique est loin de se réduire à la recherche de démonstrations et à la vérification de celles-ci. La confiance que la communauté mathématique place dans un de ses membres qui propose un résultat nouveau intervient dans la réception qu'aura ce résultat, et ce d'autant plus s'il est inattendu, ou modifie la façon de voir les choses. On peut prendre pour exemple historique les controverses sur les géométries non euclidiennes au XIX^e siècle, durant lequel les travaux de Lobatchevski ont été largement ignorés ; ou bien, dans un autre ordre d'idée, la difficulté de la réception des travaux du jeune républicain Galois au début du même siècle, notamment par Cauchy. La sociologie des mathématiques étudie de tels phénomènes (voir sociologie des sciences).

Augustin Louis Cauchy.

D'autre part, la solidité même des bases ne peut reposer sur les seules mathématiques. En effet les théorèmes d'incomplétude, démontrés par Kurt Gödel dans la première moitié du XX^e siècle, montrent que, contrairement à ce qu'espérait David Hilbert, il est impossible de réduire formellement les bases des mathématiques en un système dont la sûreté se démontre à partir de celles-ci, et cela entraîne que certaines propriétés considérées « vraies » resteront inaccessibles à la démonstration, quels que soient les axiomes choisis.