Mathématiques du Sudoku - Définition
La liste des auteurs de cet article est disponible ici.
Nombre de solutions possibles
La réponse à la question « Combien y a-t-il de Sudoku ? » dépend de la définition d'une solution et de l'équivalence entre plusieurs solutions. Pour l'énumération de toutes les solutions possibles (ie. grilles complètes), on retient la définition suivante :
Une grille A est différente d'une grille B, si la valeur de la case en A(i, j) est différente de B(i, j), pour tout i, j (valeurs limitées par la dimension de la grille).
Si une grille A est obtenue par symétrie de la grille B alors elles sont considérées comme différentes. Les rotations sont également comptées comme de nouvelles solutions.
Énumérations des solutions symétriquement distinctes
Deux grilles sont dites symétriquement distinctes si l'une ne peut être dérivée de l'autre (par une ou plusieurs opérations de préservation de la symétrie).
Préservation de la symétrie
Les opérations suivantes transforment toujours une grille valide en une autre grille valide :
- changer le label de chaque symbole (9!)
- permutations des bandes (3!)
- permutations des piles (3!)
- permutations des lignes dans une bande (3!3)
- permutations des colonnes dans une pile (3!3)
- réflexion, transposition, rotation de 90° (avec l'une de ces opérations et les permutations, il est possible de déduire les autres opérations, ce qui fait que ces opérations ne contribuent qu'avec un facteur de 2).
Ces opérations définissent une relation de symétrie entre deux grilles équivalentes. En excluant le changement de labels, et en considérant les 81 valeurs présentes dans la grille, ces opérations forment un sous-groupe du groupe symétrique S81 avec un ordre 3!8×2 = 3359232.
Identifier les solutions grâce au lemme de Burnside
Pour une solution, l'ensemble des solutions équivalentes qui peut être obtenu en utilisant ces opérations (sauf le renommage des valeurs), forme une orbite du groupe symétrique. Le nombre de solutions symétriquement distinctes est ainsi le nombre d'orbites, une valeur qui peut être calculée grâce au lemme de Burnside. Les points fixes de la méthode de Burnside sont des solutions qui ne diffèrent que par le renommage. Grâce à cette technique, Jarvis Russell a calculé le nombre de solutions symétriquement distinctes : 5 472 730 538.
Bandes du Sudoku
Pour des valeurs L et C larges, la méthode de Kevin Kilfoil (généralisée par la suite) est utilisée pour estimer le nombre de façons de compléter une grille. Cette méthode part du principe que les contraintes sur lignes et les colonnes sont, pour une première approximation, des variables aléatoires conditionnellement indépendantes eu égard à la contrainte sur la région. Des calculs algébriques permettent d'aboutir à la formule de Kilfoil-Silver-Pettersen :
où bL, C est le nombre de manières de compléter un Sudoku avec L régions (d'une taille de LxC) horizontalement adjacentes. L'algorithme de Pettersen, implémenté par Silver est actuellement la technique la plus rapide connue pour évaluer de manière exacte les valeurs bL, C.
Le compte des bandes pour les problèmes dont "le nombre total de grilles de Sudoku est inconnu" est donné ci-dessous. Comme dans le reste de cet article, les dimensions correspondent à celles des régions.
-
Dimensions Nombre de bandes Auteur(s) Vérification formelle 2×C (2C)! (C!)2 (obvious result) Oui 3×C 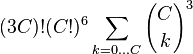
Pettersen Oui 4×C (voir ci-dessous pour le résultat mathématique) Pettersen Oui 4×4 16! × 4!12 × 1273431960 = c. 9.7304×1038 Silver Oui 4×5 20! × 5!12 × 879491145024 = c. 1.9078×1055 Russell Oui 4×6 24! × 6!12 × 677542845061056 = c. 8.1589×1072 Russell Oui 4×7 28! × 7!12 × 563690747238465024 = c. 4.6169×1091 Russell Oui (des calculs jusqu'à 4×100 ont été effectués par Silver, mais ne sont pas indiqués ici) 5×3 15! × 3!20 × 324408987992064 = c. 1.5510×1042 Silver Oui# 5×4 20! × 4!20 × 518910423730214314176 = c. 5.0751×1066 Silver Oui# 5×5 25! × 5!20 × 1165037550432885119709241344 = c. 6.9280×1093 Pettersen/Silver Non 5×6 30! × 6!20 × 3261734691836217181002772823310336 = c. 1.2127×10123 Pettersen/Silver Non 5×7 35! × 7!20 × 10664509989209199533282539525535793414144 = c. 1.2325×10154 Pettersen/Silver Non 5×8 40! × 8!20 × 39119289737902332276642894251428026550280700096 = c. 4.1157×10186 Pettersen/Silver Non
- # : même auteur mais avec une autre méthode
L'expression pour le cas 4×C est :
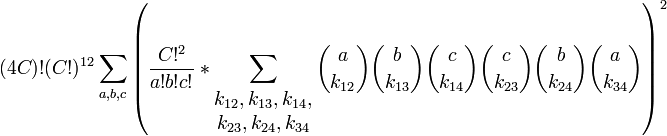
avec :
- la somme extérieure s'applique sur tous les a,b,c tel que 0⇐a,b,c et a+b+c=2C
- la somme intérieure s'applique sur tous les k12,k13,k14,k23,k24,k34 = 0 tel que
- k12,k34 = a et
- k13,k24 = b et
- k14,k23 = c et
- k12+k13+k14 = a-k12+k23+k24 = b-k13+c-k23+k34 = c-k14+b-k24+a-k34 = C
Sudoku avec des contraintes additionnelles
Plusieurs types de contraintes existent sur des Sudokus avec des régions de 3x3. Les noms n'ayant pas été standardisés, les liens externes pointent vers les définitions :
| Type | Nombre de grilles | Auteur(s) | Vérification formelle |
|---|---|---|---|
| 3doku | 104015259648 | Stertenbrink | Oui |
| Disjoint Groups | 201105135151764480 | Russell | Oui |
| Hypercube | 37739520 | Stertenbrink | Oui |
| Magic Sudoku | 5971968 | Stertenbrink | Oui |
| Sudoku X | 55613393399531520 | Russell | Oui |
| NRC Sudoku | 6337174388428800 | Brouwer | Oui |
Tous les Sudokus sont valides (unicité des nombres dans les lignes, colonnes et régions) après l'application des opérations qui préservent les propriétés du groupe du Sudoku. Certains Sudoku sont spéciaux dans le sens où certaines opérations ont le même effet que le renommage des chiffres :
| Transformation | Nombre de grilles | Auteur(s) | Vérification formelle |
|---|---|---|---|
| Transposition | 10980179804160 | Russell | Indirectement |
| Quart de tour | 4737761280 | Indirectement | |
| Moitié de tour | 56425064693760 | Indirectement | |
| Permutation des bandes | 5384326348800 | Indirectement | |
| Permutations des lignes dans les bandes | 39007939461120 | Indirectement |