Longueur d'un arc - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie, la question de la longueur d'un arc est intuitivement simple à concevoir. L'idée d'arc correspond à celle d'une ligne, ou d'une trajectoire d'un point dans un plan ou l'espace par exemple. Sa longueur peut être vue comme la distance parcourue par un point matériel suivant cette trajectoire ou encore comme la longueur d'un fil prenant exactement la place de cette ligne. La longueur d'un arc est, soit un nombre positif, soit l'infini.
Un vieil exemple est celui du demi-cercle de rayon r, où r désigne un nombre réel positif. Sa longueur est égale à πr. Un exemple, plus simple, est donné par un segment, sa longueur est égale à la distance qui sépare ses deux extrémités.
Selon l'époque, différentes méthodes permettent de définir et de mesurer la longueur d'un ensemble d'arcs de plus en plus vaste. Eudoxe de Cnide, un mathématicien grec du IVe siècle av. J.-C., puis Archimède utilisent une méthode, dite d'exhaustion pour calculer celle d'un arc de cercle. La physique de la fin du XVIIe siècle développe une nouvelle approche, fondée sur les progrès réalisés en mécanique du point grâce en particulier au calcul infinitésimal appliqué à l'astronomie. La longueur d'un arc est perçue comme le produit du temps nécessaire à un point matériel pour parcourir l'arc par sa vitesse, si elle est supposée constante. Cette définition est généralisée par Bernhard Riemann et devient la pierre angulaire pour construire une distance sur de nouvelles géométries, maintenant appelées variétés riemanniennes.
Pour le mathématicien français Camille Jordan , ces définitions sont trop restrictives. Il s'intéresse aux propriétés d'une courbe fermée, c'est-à-dire un arc dont le point initial se confond avec le point final. La définition précédente, issue de la physique deux siècles plus tôt, suppose que l'arc soit dérivable. Cette limitation empêche l'usage d'un vaste arsenal de méthodes, pourtant indispensables à la résolution de nombreuses questions. Il propose une nouvelle définition, à l'aide d'une borne supérieure et de la longueur d'une ligne polygonale. C'est maintenant celle la plus communément utilisée. Pour Hermann Minkowski , les idées de Jordan sont peu adaptées à ses besoins. Dans le contexte des questions qu'il se pose, la longueur qu'il cherche à définir est surtout celle de la frontière d'une surface. Un cercle est défini comme l'ensemble des points P d'un disque tels que tout voisinage de P contient un point du disque et un point extérieur. Il définit la longueur à l'aide de la notion intuitive de tube, correspondant à l'ensemble des points situés à une distance inférieure à r d'un point de l'arc. Cette définition se prête à de nombreuses généralisations, qui permettent même de donner un sens à la longueur d'une courbe fractale.
Premiers calculs
L'une des mesures de longueur la plus célèbre et la plus ancienne est celle d'un demi arc de cercle de rayon 1. Cette longueur, notée π est calculée depuis bien longtemps. Pour les babyloniens, sa valeur se calcule grâce à la relation qui relie l'aire du cercle avec le périmètre du demi-arc, il trouve l'approximation 3 + 1/8.
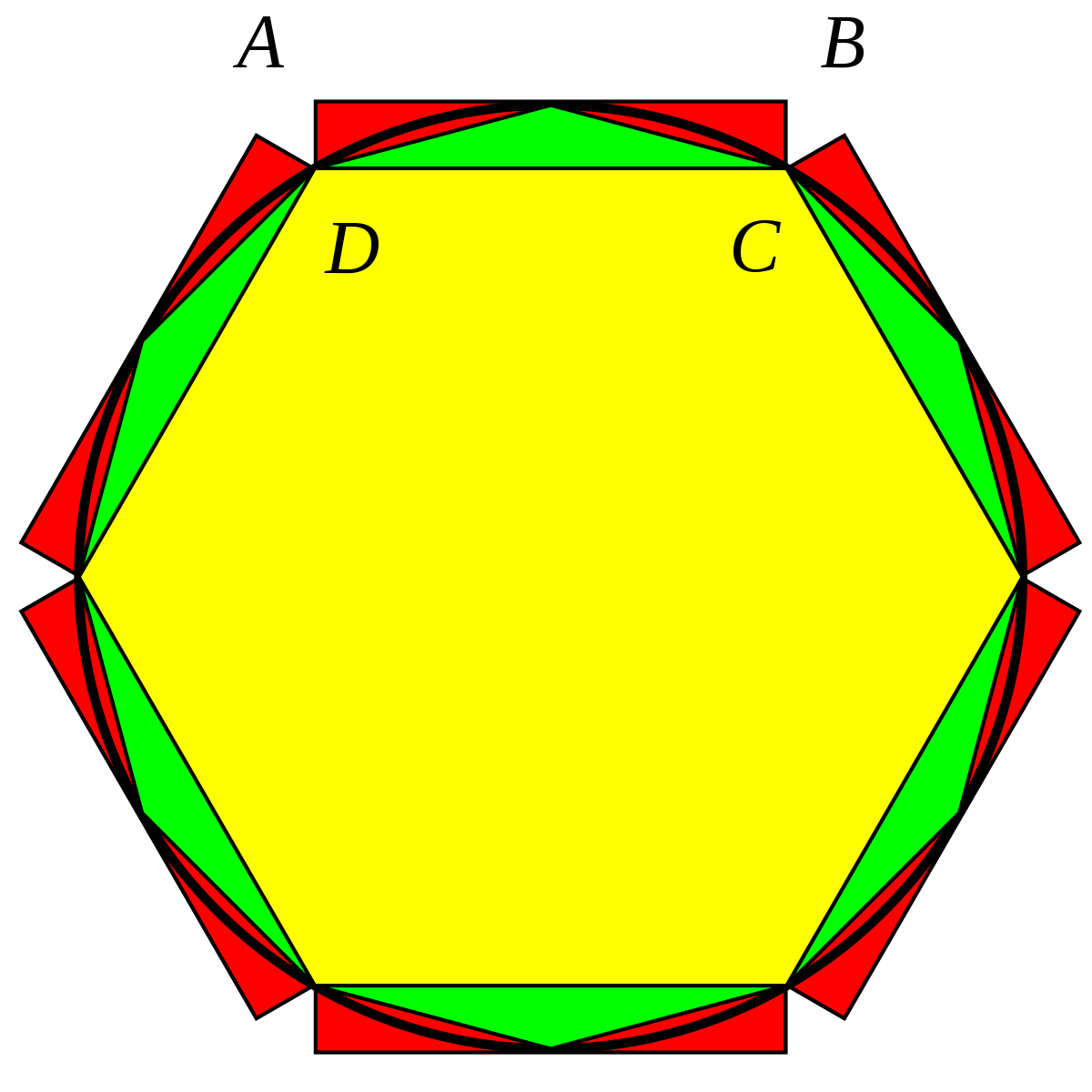
Un progrès théorique important est l'œuvre d'Archimède. Pour le physicien, un polygone convexe dont les sommets sont des points du cercle est de périmètre plus petit que celui du cercle. En effet, il est plus court, pour rejoindre deux sommets consécutifs de passer par l'arête (le segment est le plus court chemin entre ses deux points d'extrémités), ce qui donne une minoration de π. Inversement, le polygone convexe régulier dont chaque milieu d'arête est un point du cercle est de périmètre plus grand. S'il ne peut démontrer cette proposition en général car il ne dispose pas d'une définition de la longueur d'un arc qui lui permettrait de réaliser cette prouesse, elle semble intuitive à l'œil, et résulte (dans le cas du cercle) de la proportionnalité entre les aires de secteurs circulaires et les arcs qui les sous-tendent. À l'aide d'un polygone régulier de 96 côtés, il démontre que la valeur de π se situe entre 3 + 1/7 et 3 + 10/71. Le principe du calcul est donné dans l'article pi.
La méthode est générale pour tout arc dont la convexité se situe toujours du même côté, c'est-à-dire dont l'arc n'est composé que de points frontières de l'enveloppe convexe. Tout ligne polygonale, dont les sommets sont situés sur l'arc, possède une longueur plus petite que celle de l'arc étudié. On dispose ainsi d'un minorant. On peut alors construire une suite de lignes polygonales de longueurs croissantes (pn) toutes plus petites que la longueur de l'arc. On construit ensuite une suite de lignes polygonales à l'extérieur de l'enveloppe convexe, dont les extrémités sont ceux de la ligne polygonale et qui longent de plus en plus précisément l'arc. La suite des longueurs (Pn) est choisie décroissante et chaque longueur est plus grande que celle de l'arc. Les seules valeurs possibles, pour la longueur de l'arc, sont situées dans le segment [pn, Pn]. La suite est construite de telle manière à ce que la distance entre pn et Pn soit de plus en plus petite à tel point que pour tout nombre strictement positif ε, il existe une valeur n tel que Pn - pn soit strictement plus petit que ε. L'intersection de tous les intervalles [pn, Pn] est réduit à un point, qui est nécessairement la longueur de l'arc. Cette méthode est dite d'exhaustion.
Elle est utilisée par le mathématicien chinois Liu Hui durant le IIIe siècle avec des approximations plus performantes que celles d'Archimède. Il trouve la valeur approchée de π égale à 3,1416. Cette méthode reste en vigueur jusqu'à la fin du XVIIe siècle et permet de trouver d'autres résultats comme la longueur d'un arc de spirale logarithmique par Torricelli en 1645 ou de cycloïde par Christopher Wren.

















































