Longueur d'un arc - Définition

Géométrie différentielle

Principe de Fermat

Le maître nageur, situé sur une plage en A₁, doit éviter une noyade située en A₂ dans la mer. Il doit pour cela trouver le point M tel que le chemin le plus rapide pour lui soit composé du segment A₁M puis MA₂, dépendant du rapport de sa vitesse sur la plage et celle dans l'eau.

Les lois de Descartes peuvent se lire comme l'ajout d'un nouvel espace métrique.

Pierre de Fermat est un des précurseurs du calcul différentiel, avant Leibniz et Newton. Il propose une astucieuse interprétation des lois de Snell-Descartes dans une lettre de 1662 et adressée à Marin Cureau de la Chambre, désormais célèbre. Fermat énonce un principe très général : « ... la nature agit toujours par les voies les plus courtes. » qui implique les règles de propagation de la lumière pour l'optique géométrique.

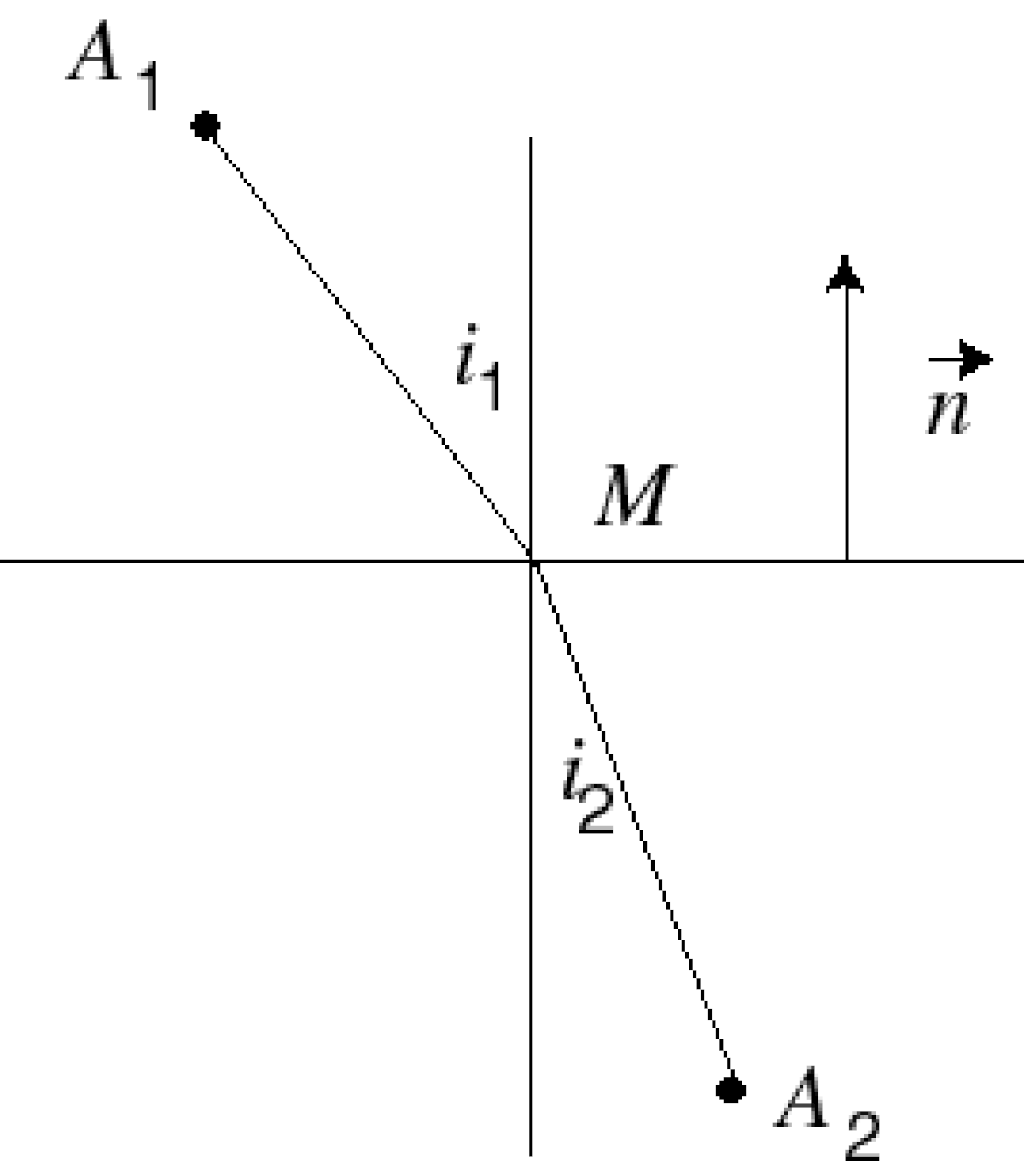
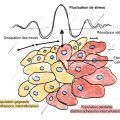
L'intuition de Fermat est exacte. La vitesse de la lumière est plus lente dans l'eau ou dans du verre que dans le vide ou dans l'air. La trajectoire de la lumière est en conséquence fonction du rapport des vitesses de la lumière dans les deux milieux. Il est possible d'illustrer ce principe par le problème dit du maître nageur, représenté sur la figure de gauche. Un maître nageur, situé au point A₁ doit éviter une noyade en A₂. Pour être le plus rapide possible, le maître-nageur doit trouver le point M situé à la frontière entre la plage et la mer tel que courir de A₁ à M, puis nager de M à A₂, soit le plus trajet le plus rapide. Comme il court plus vite qu'il ne nage, le point M se trouve nécessairement plus proche de A₂ que le point du segment A₁A₂ à la frontière de la plage et de la mer.

Une autre manière de modéliser cette question est d'équiper l'espace d'une nouvelle distance d₂, associée à la vitesse de déplacement de la lumière ou de celle du maître-nageur. La distance entre deux points est donnée par le temps nécessaire pour aller d'un point à un autre. Si C est un arc géométrique de paramétrage (I, f), et n_A le rapport entre la vitesse du maitre nageur sur la plage et celle au point A, la longueur de l'arc C s'exprime par :

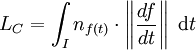
C'est maintenant la longueur d'un arc qui permet de définir la distance d₂ : la distance entre deux points est la plus petite longueur d'un arc reliant ces deux points. La figure de droite illustre la géométrie de l'espace, vue avec les deux distances. L'espace équipé de la distance d₂ est illustré en haut. Les trajectoires les plus courtes pour le maitre nageur sont les droites représentées en vert, et les points à égale distance de sa position sont les arcs de cercle, en rouge sur la plage et en bleu dans la mer. Cette même figure est reproduite sur la figure du bas, cette fois avec la distance usuelle. Comme le maître nageur est moins rapide dans l'eau, les portions de cercles dans la mer sont écrasées. Ce tassement déforme les portions de droites vertes qui se trouvent dans l'eau. Les angles obtenus, entre un segment vert sur la plage et son prolongement dans l'eau, suivent les lois de Descartes.

Principe de moindre action

En mécanique, le principe de Fermat porte souvent le nom de principe de moindre action. Il est illustré ici pour la résolution du problème brachistochrone.

L'expression utilisée par Fermat pour décrire son principe est habile. Rien n'indique, dans sa formulation, qu'il est limité à l'optique géométrique. L'avenir lui donne raison. Une question, déjà abordée par Galilée sans succès en 1638, consiste à trouver la courbe que doit emprunter un point matériel glissant sans frottement pour aller le plus rapidement possible d'un point A à un point B. Le point B est supposé se trouver à une altitude plus petite ou égale à celle du point A pour que la question ait une solution. Cette question porte le nom de problème brachistochrone. Elle est remis à l'honneur par Jean Bernoulli en 1696 et posée comme défi aux lecteurs du journal Acta Eruditorum.

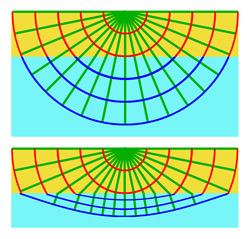
Une solution consiste encore à appliquer le principe de Fermat. Si la distance entre deux points A et B est mesurée par le temps nécessaire pour aller du plus haut au plus bas, l'espace est cette fois dilaté de manière parabolique sur l'axe vertical. En effet, si on appelle 1 la longueur parcourue verticalement en 1 unité de temps, la longueur parcourue verticalement en 2 unités de temps est de 4, puis celle parcourue en 3 est de 9 etc... Résoudre le problème brachistrochrone revient à trouver les lois de passage entre l'espace mesuré par la vitesse du point matériel et celui mesuré de la manière usuelle. La réponse est illustrée sur la figure de droite. Comme précédemment la figure du dessus représente l'espace mesurée à l'aide de la distance d₂, correspondant à la vitesse du point matériel. On considère les trajectoires, vues avec la distance d₂ comme des demis droites issues d'un même point, où la vitesse du point est initialement nulle. Ces demi-droites sont régulièrement espacées d'un angle de π/8 sur la figure. En rouge sont indiquées les positions possibles du point au bout d'un temps fixe et régulier, 1, 2, 3 et 4 secondes. Les courbes rouges correspondent à ce que l'on appelle usuellement des demi-cercles.

Cette même figure, vue avec la distance usuelle est illustrée sous la première. Elle est un peu plus difficile à lire que celle correspondant à la géométrie précédente. Le plus simple est de commencer par la ligne verte numérotée 1. Elle correspond à un déplacement horizontal. Comme le point matériel possède une vitesse initiale nulle, son déplacement est nul et la droite est transformé en un point, noté 1 sur la figure du bas. La trajectoire noire correspond à une courbe dont la tangente initiale est verticale. Il n'existe pas une courbe possible, mais une infinité, dont deux sont illustrées sur la figure du bas, en noir. Ces courbes correspondent à des arches complètes de cycloïde. Toute arche de cycloïde de point initial celui de la figure correspond à une droite de tangente initiale verticale avec la distance d₂. Cette situation est analogue pour l'image de toutes les demi-droites vertes de la figure supérieure. Ainsi, la demi-droite numéroté 2 correspond à une portion de cycloïde illustrée sur la partie basse de la figure, et toute homothétie de cette portion de cycloïde correspond aussi à une image de la demi-droite 2.

La technique utilisée pour résoudre le problème brachistochrone est de même nature que celle du paragraphe précédent en optique. On cherche l'arc le plus court pour une distance bien choisie. Le principe de Fermat prend parfois le nom de principe de moindre action, que Maupertuis redécouvre et énonce ainsi : « L'Action est proportionnelle au produit de la masse par la vitesse et par l'espace. Maintenant, voici ce principe, si sage, si digne de l'Être suprême : lorsqu'il arrive quelque changement dans la Nature, la quantité d'Action employée pour ce changement est toujours la plus petite qu'il soit possible. »

Variété riemannienne

La définition de Riemann de la longueur d'un arc est le fondement d'une nouvelle manière de définir la distance.

Dans l'exemple du problème brachistochrone, l'équivalent de l'indice de réfraction correspond un facteur de compression de l'espace, à l'image de l'exemple d'optique. Comme ici l'espace a plutôt tendance à se dilater, l'indice est rapidement compris entre 0 et 1. Il est précisément égal à (2gh)^-1/2 si h est l'altitude, compté négativement. Pour résoudre l'équation différentielle de Newton, indiquant la trajectoire des planètes, la même méthode s'applique avec un coefficient cette fois ci, égal à a/h. Les calculs sont un peu plus simples et les arches de cycloïdes sont transformées en demi-cercles.

Une surface ayant en un point une courbure négative, ressemble localement à une selle de cheval.

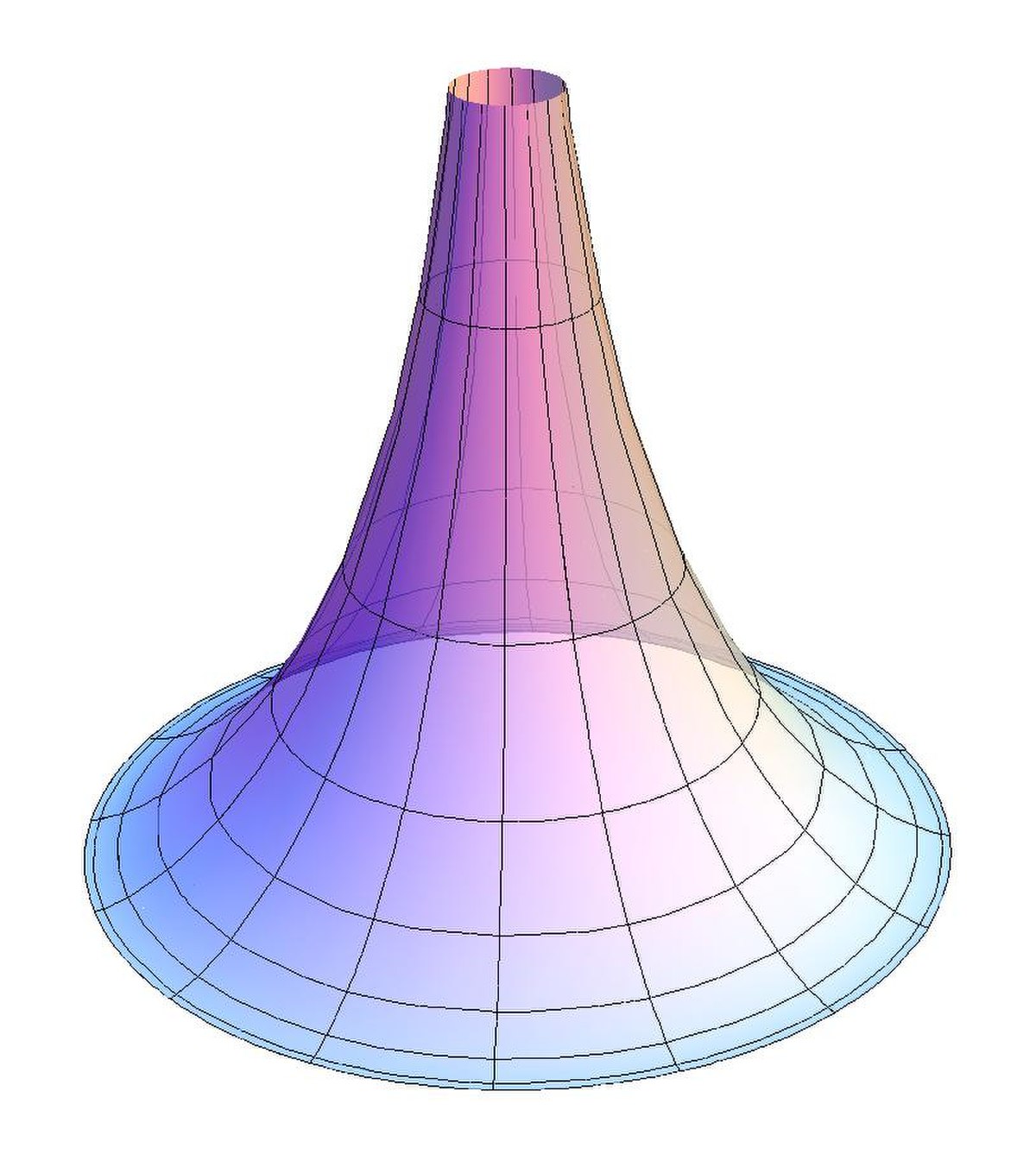
Si Bernhard Riemann, un élève de Gauss s'intéresse suffisamment à cette question pour en faire son sujet de thèse, ce n'est pas pour proposer une nouvelle méthode de résolution d'une célèbre équation différentielle, mais pour mieux comprendre la géométrie. Si l'on retire les points d'altitude 0 (un point d'altitude 0 est en effet à une distance non nulle de lui-même, ce qui ne fait guère sens), on obtient un espace métrique. Pour définir cette métrique, on commence par une nouvelle définition de la longueur L_C d'un arc C de l'espace G qui, s'il est paramétré par (I, f) vaut dans le cas particulier étudié :

Chaque point p de G possède un espace tangent T_p, muni d'un produit scalaire et donc d'une norme. Dans le cas particulier du paragraphe, la norme est celle du plan, que multiplie le facteur de compression n_p proportionnel à l'inverse de l'altitude de p. La définition de la longueur d'un arc permet ensuite de définir la distance entre deux points. Elle est égale à la longueur du plus petit arc reliant ces deux points.

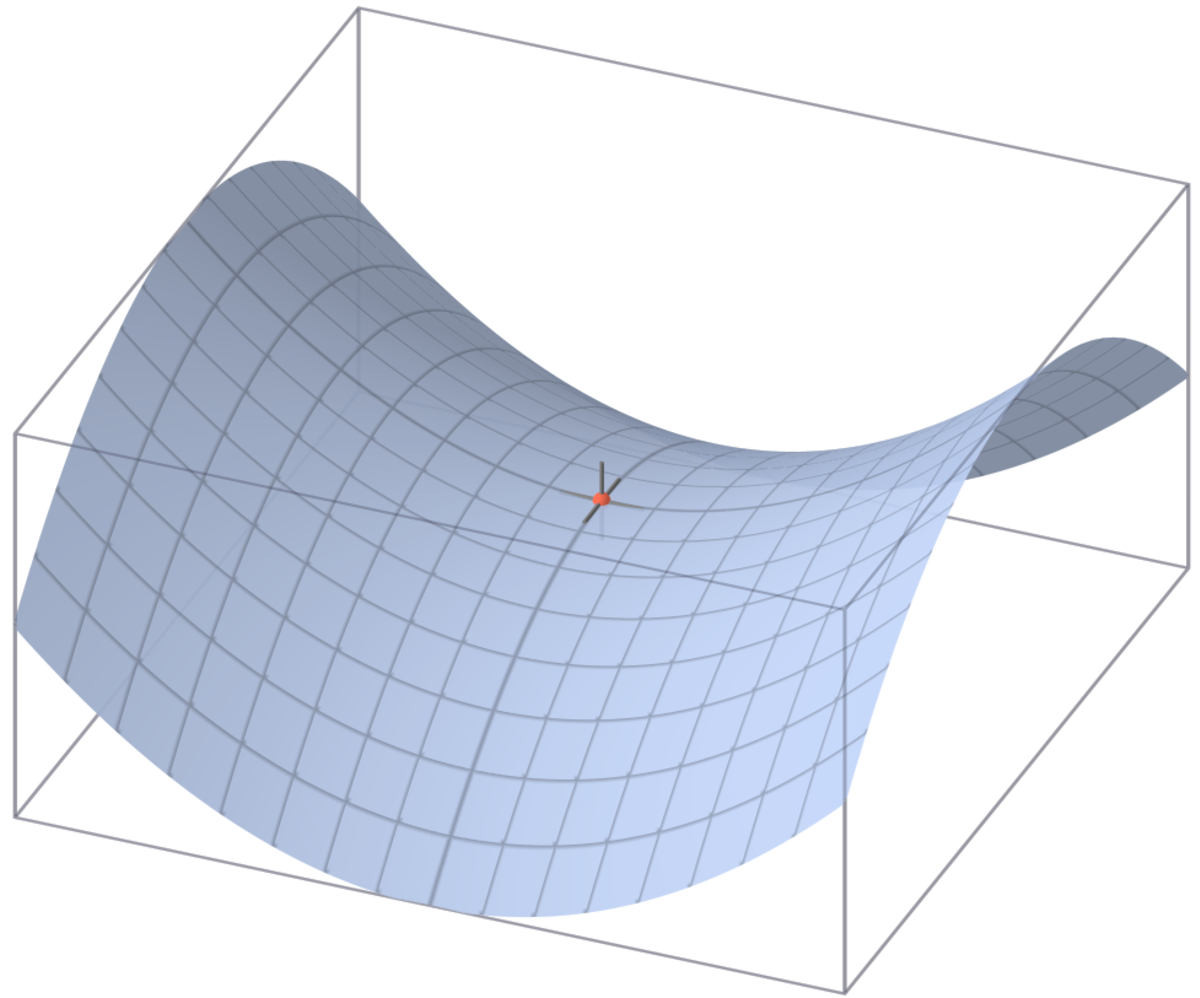
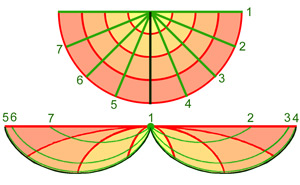
Qualitativement, l'espace que l'on vient de définir ressemble un peu à la figure de droite. Le formalisme de Riemann, consistant à d'abord définir la longueur d'un arc puis la distance, est finalement très puissant. Il permet de définir un large ensemble de géométries, dans lequel les concepts classiques comme les droites (qui prennent le nom de géodésiques) les cercles ou les courbures s'étendent. Cette méthode permet de définir des surfaces qui n'existent pas en dimension 3. Celle considérée dans ce paragraphe possède une courbure constante négative. La courbure en un point p correspond au produit des deux courbures les plus extrêmes que peuvent prendre les arcs paramétrés à l'aide d'une abscisse curviligne au point p. Si les deux cercles osculateurs se trouvent sur un ellipsoïde, on parle de courbure positive. s'ils se trouvent sur une selle de cheval, on parle de courbure négative. Aucune surface en dimension 3 ne possède de courbure négative constante, raison pour laquelle la géométrie décrite dans ce paragraphe n'est pas exactement celle de la figure de droite.

Calcul des variations

Les trois paragraphes précédents ont un point commun, pour être opérationnel, ils nécessitent la capacité de trouver le plus court chemin entre deux points d'une surface ou d'une géométrie particulière, ce qui n'est pas, en général une question facile.

Un optimum possède un gradient nul.

L'équation d'Euler-Lagrange détermine le gradient qui, à un espace de courbes associe sa longueur.

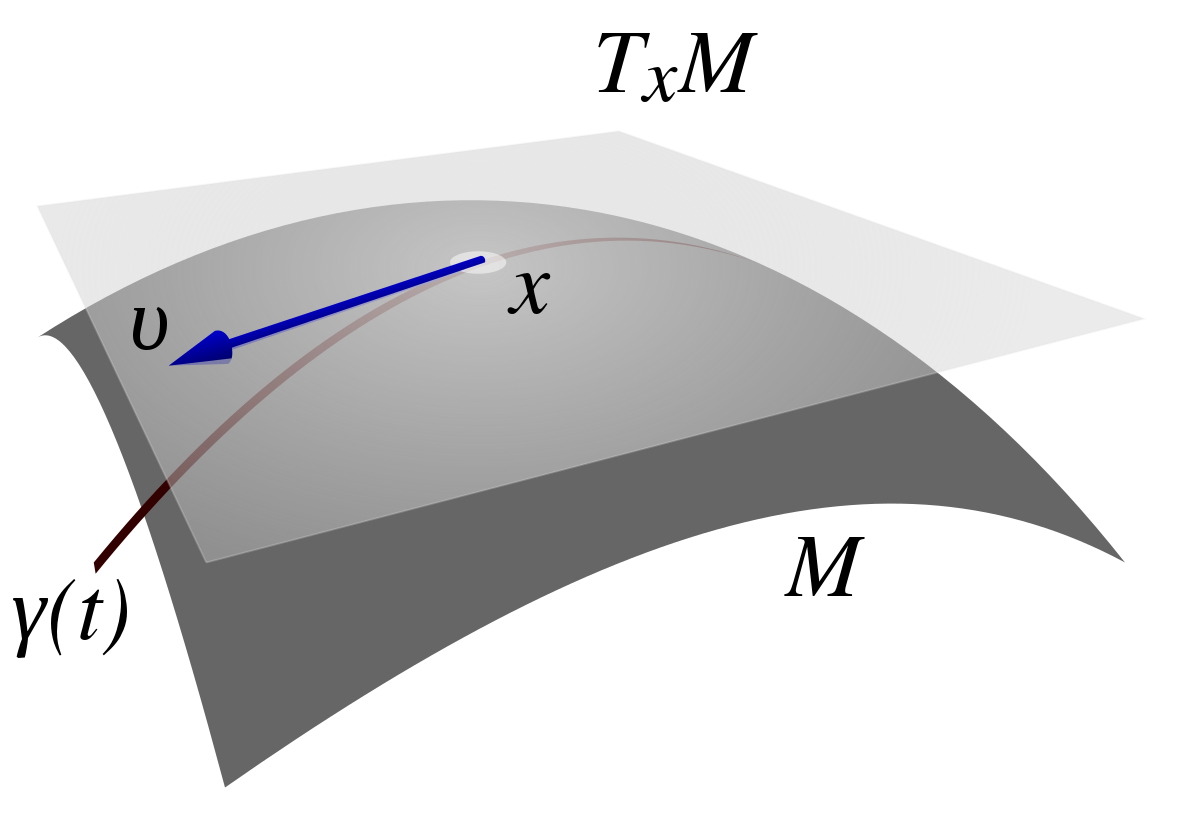
La méthode la plus fructueuse s'apparente à celle de la géométrie différentielle. En dimension finie, et sous les bonnes hypothèses, un point optimal possède une approximation linéaire tangente plate, illustrée sur la figure de gauche. En terme mathématiques, cela signifie que le gradient de la fonction à optimiser est nul sur un point extrémal.

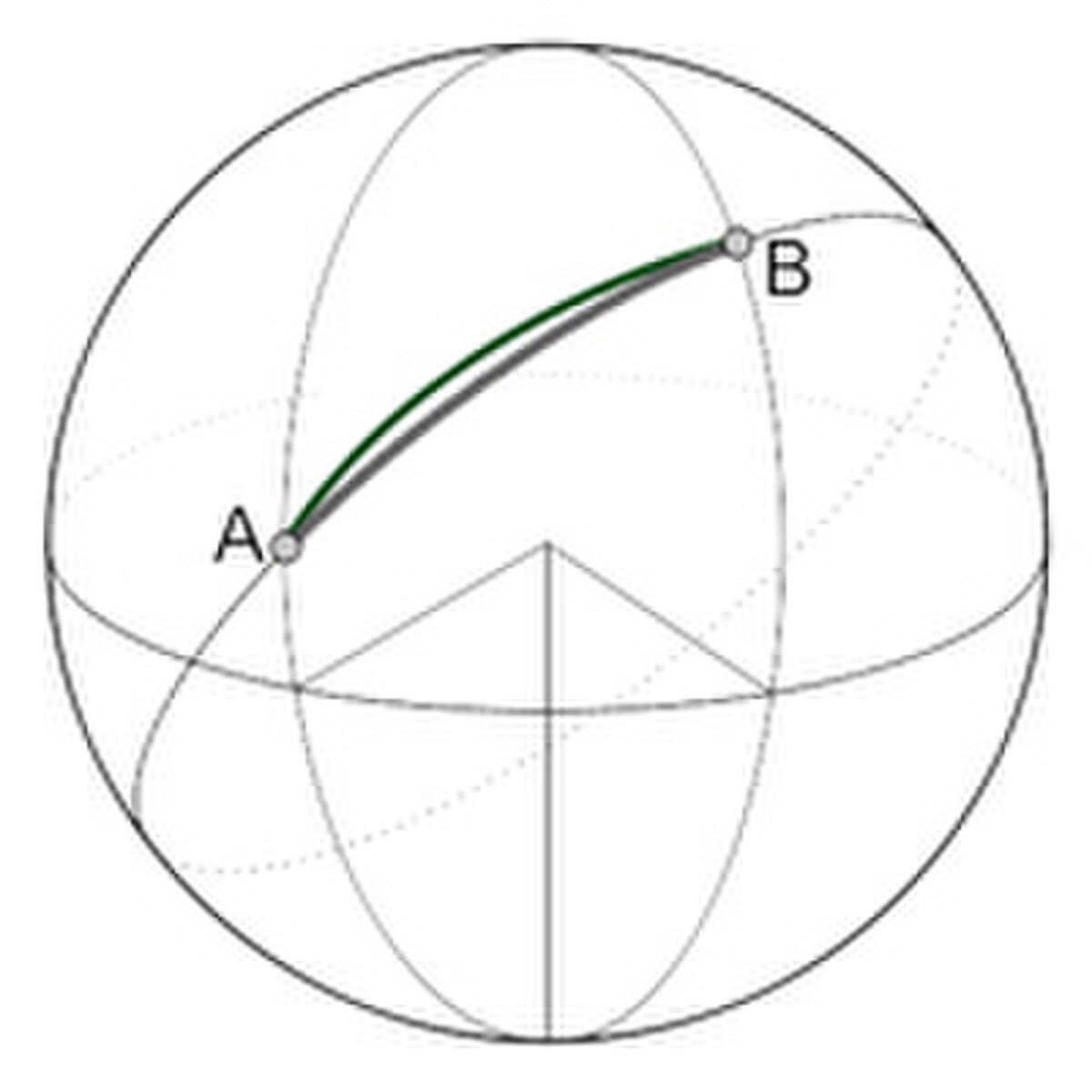
C'est une méthode de cette nature qu'utilise Bernoulli pour résoudre le problème brachistochrone. Elle est illustrée sur la figure de droite, une petite variation autour du chemin optimal ne change pas sa longueur, au premier ordre. Ainsi le chemin proche de l'optimal, illustré en vert, est au premier ordre, de même longueur que la courbe optimale, illustrée en gris. Leonhard Euler affine la méthode et propose une première démonstration de la résolution du problème isopérimétrique consistant à trouver l'arc fermé d'une longueur donnée et enserrant une surface de plus grande aire possible (La démonstration d'Euler est proposée dans l'article Multiplicateur de Lagrange). En 1755 Lagrange écrit une lettre à Euler. Elle porte sur le calcul de la courbe tautochrone, correspondant à une question analogue au problème brachistochrone. Cette correspondance est le début d'un long un travail commun et permet d'établir l'équation d'Euler-Lagrange, une méthode très générale pour trouver les géodésiques.

Si l'équation d'Euler-Lagrange est suffisante pour résoudre le problème tautochrone, il est parfois nécessaire de l'enrichir, par exemple pour trouver la courbe de la chaînette, c'est-à-dire la position qu'occupe au repos un câble de masse linéaire constante, soumis à la gravité. La méthode est enrichie par celle du multiplicateur de Lagrange.

Les mathématiques du XVIII^e siècle sont encore insuffisantes pour démontrer rigoureusement la pertinence des calculs d'Euler et de Lagrange. Leur connaissance en analyse fonctionnelle est encore bien trop limitée. Ces méthodes, qui prennent le nom de calcul des variations, deviennent vraiment rigoureuses sous l'influence de Karl Weierstrass au XIX^e siècle et surtout les travaux de Banach et Sobolev au XX^e siècle.

Espace de Sobolev

Posons la question en termes flous : deux courbes « proches » ont-elles des longueurs voisines ?

Voici un exemple négatif. On prend le graphe de la fonction constante égale à 0 sur [0,1]. Celui-ci est de longueur 1. On fabrique facilement une suite de fonctions continues sur [0,1], rectifiables, qui converge uniformément vers f et dont la longueur ne converge pas vers 1.

Par exemple : f₁ est une fonction triangle avec des pentes 1 sur [0,1/2] et -1 sur [1/2,1]. Puis f₂ est une fonction formée de deux triangles, avec des pentes 1 sur [0,1/4], -1 sur [1/4,1/2], 1 sur [1/2,3/4], -1 sur [3/4,1], et ainsi de suite (4,8,16 triangles, ...). Chacune des fonctions f_n a un graphe de longueur , et par ailleurs il y a bien convergence uniforme vers f.

Pour obtenir des résultats de continuité pour l'application « longueur », il ne faut donc pas travailler avec la norme de la convergence uniforme. Il faudrait plutôt une norme du type de celles des espaces de Sobolev.